集成学习

1.集成学习

集成学习是一种“博采众长”的思想，他通过构建并结合多个机器学习模型来完成学习任务。假如我们通过训练得到了两个学习器，一个学习器准确率为90%，另一个只有60%，但是对于某一些样本，60%的那个学习器的表现可能会比90%的那个好一些。所以集成学习就是组合多个分类器，最后得到一个更好的分类器。对于训练集，通过训练若干个个体学习器，通过一定的结合策略，最终形成一个强学习器，以达到博采众长的目的。
集成学习算法：
1.个体学习器之间不存在强依赖关系，装袋（bagging）
2.随机森林（Random Forest）
3.个体学习器之间存在强依赖关系，提升（boosting）
4.Stacking

2.bagging

bagging也叫做bootstrap aggregating，是在原始数据集选择S次后得到S个新数据集的一种技术。是一种又放回的抽样。对于m个样本的原始数据集，我们每次先随机采集一个样本放入采样集，接着把该样本放回，这样采集m次，最终可得到m个样本的采样集，

bagging的学习如下图所示：

代码：

from sklearn import neighbors
from sklearn import datasets
from sklearn.ensemble import BaggingClassifier#导入bagging
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt

iris=datasets.load_iris()
x_data=iris.data[:,:2]#这里只取前两个特征，如果全部取得的话训练出的模型效果较好，bagging效果不明显
y_data=iris.target

x_train,x_test,y_train,y_test=train_test_split(x_data,y_data)

knn=neighbors.KNeighborsClassifier()
knn.fit(x_train,y_train)

KNeighborsClassifier()

def plot(model):
    #获取数据取值范围
    x_min,x_max=x_data[:,0].min()-1,x_data[:,0].max()+1
    y_min,y_max=x_data[:,1].min()-1,x_data[:,1].max()+1

    #生成网格矩阵
    xx,yy=np.meshgrid(np.arange(x_min,x_max,0.02),
                      np.arange(y_min,y_max,0.02))
    z=model.predict(np.c_[xx.ravel(),yy.ravel()])
    z=z.reshape(xx.shape)
    cs=plt.contourf(xx,yy,z)

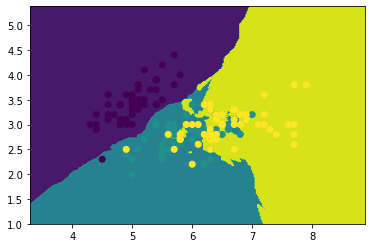
plot(knn)
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()
knn.score(x_test,y_test)#准确率

​

​

0.7631578947368421

dtree=tree.DecisionTreeClassifier()#决策树
dtree.fit(x_train,y_train)

DecisionTreeClassifier()

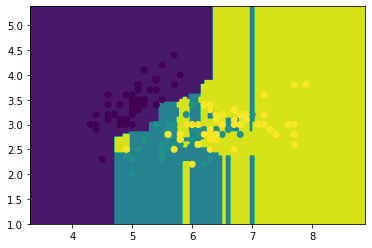
plot(dtree)
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()
dtree.score(x_test,y_test)

​

​

0.631578947368421

bagging_knn=BaggingClassifier(knn,n_estimators=100)#训练100个knn模型
#输入数据建立模型
bagging_knn.fit(x_train,y_train)
plot(bagging_knn)
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()
bagging_knn.score(x_test,y_test)

​

0.7894736842105263

bagging_tree=BaggingClassifier(dtree,n_estimators=100)
bagging_tree.fit(x_train,y_train)
plot(bagging_tree)
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()
bagging_tree.score(x_test,y_test)

​

​

0.6578947368421053

注意每次运行由于会对数据集随机切分，所以每次运行出来的 结果也会不相同，而且集成学习后的结果也未必会比原来的好，可能相等也可能会下降。

3.随机森林

RF=决策树+Bagging+随机属性选择

随机森林得到流程：
1.样本的随机：从样本集中使用bagging的方式，随机选择n个样本
2.特征的随机：从所有属性d中随机选择k（k<d）个属性,然后从k个属性中选择最佳分割属性作为节点建立CART决策树
3.重复以上两个步骤，建立m棵CART决策树。
4.这m棵CART决策树形成随机森林，通过投票标记结果，决定数据属于哪一类。

程序

from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import numpy as np
import matplotlib.pyplot as plt

部分数据集

[root@iZbp173czfyjpvvdm6k4amZ data]# cat LR-testSet2.txt 
0.051267,0.69956,1
-0.092742,0.68494,1
-0.21371,0.69225,1
-0.375,0.50219,1
-0.51325,0.46564,1
-0.52477,0.2098,1
-0.39804,0.034357,1
-0.30588,-0.19225,1
0.016705,-0.40424,1
0.13191,-0.51389,1
0.38537,-0.56506,1
0.52938,-0.5212,1
0.63882,-0.24342,1

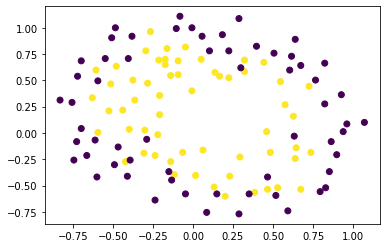
data=np.genfromtxt("/root/jupyter_projects/data/LR-testSet2.txt",delimiter=",")
x_data=data[:,:-1]
y_data=data[:,-1]
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()

​
​

def plot(model):
    x_min,x_max=x_data[:,0].min()-1,x_data[:,0].max()+1
    y_min,y_max=x_data[:,1].min()-1,x_data[:,1].max()+1

    xx,yy=np.meshgrid(np.arange(x_min,x_max,0.02),
                       np.arange(y_min,y_max,0.02))
    z=model.predict(np.c_[xx.ravel(),yy.ravel()])#ravel 将多维数据转一维
    z=z.reshape(xx.shape)

    cs=plt.contourf(xx,yy,z)

    plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
    plt.show()

x_train,x_test,y_train,y_test=train_test_split(x_data,y_data,test_size=0.2)

detree=tree.DecisionTreeClassifier()
detree.fit(x_train,y_train)
plot(detree)
detree.score(x_test,y_test)

​

​

0.7083333333333334

RF=RandomForestClassifier(n_estimators=50)#默认100次
RF.fit(x_train,y_train)
plot(RF)
RF.score(x_test,y_test)

​

0.75

4.boosting

AdaBoost 是英文”adaptive Boosting“（自适应增强）的缩写，他的自适应在于：前一个基本分类器被错误分类的样本的权重会增大，而正确分类的样本的权重会减小，并再次用来训练下一个基本分类器。同时，在每一轮迭代中，加入一个新的弱分类器，直到达到某个预定的足够小的错误率或者达到预先指定的最大迭代次数才确定最终的强分类器。
如下图所示：每次从训练集中抽取一个样本组成新的样本，如果第一次4判断错误，则下一次4被抽到的概率就会增加，第二次仍然错误的话，第三次被抽到的概率就会更大。

Adaboost 算法步骤：
①首先，初始化训练数据的权重分别D1，假设N个训练样本数据，则每一个训练样本最开始是，都被赋予相同的权值：$w_{1}=\frac{1}{N}$
②然后，训练若分类器h.具体训练过程中：如果某个训练样本点被若分类器h准确的分类，那么在构造下一个训练集中，它对应的权值要减小。相反，如果某个训练样本被错误的分类，那么它对应的权值就应该增大。权值更新过的样本被用于训练下一个分类器，整个训练过程如此迭代的进行下去。
③最后，将各个训练得到的若分类器组合成一个强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权值，使其在最终的分类函数中起着较大的决定作用，而降低分类误差大的若分类器的权值，时期在最终的分类函数中起着较小的决定作用。即误差率大的分类器在最终分类中占的权重高。

Adaboost训练过程（注意不同版本用的权重更新计算方式不同）
版本1：


版本二：

程序：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.ensemble import AdaBoostClassifier#Adaboost
from sklearn.datasets import make_gaussian_quantiles#生成数据
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split

#生成二维正态分布，生成的数据分为两类，500个样本，2个样本特征
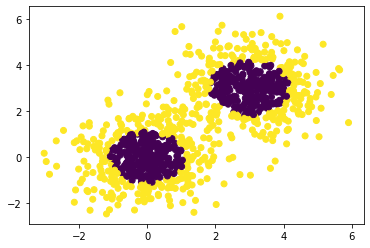
x1,y1=make_gaussian_quantiles(n_samples=500,n_features=2,n_classes=2)
#生成二维正态分布，生成的数据分为两类，500个样本，2个样本特征均值都为3
x2,y2=make_gaussian_quantiles(mean=(3,3),n_samples=500,n_features=2,n_classes=2)

x_data=np.concatenate((x1,x2))
y_data=np.concatenate((y1,-y2+1))#对数据做下处理
plt.scatter (x_data[:,0],x_data[:,1],c=y_data)
plt.show()

​

​

#不对y做处理
plt.scatter(x_data[:,0],x_data[:,1],c=np.concatenate((y1,y2)))
plt.show()

​

​

def plot(model):
    x_min,x_max=x_data[:,0].min()-1,x_data[:,0].max()+1
    y_min,y_max=x_data[:,1].min()-1,x_data[:,1].max()+1

    xx,yy=np.meshgrid(np.arange(x_min,x_max,0.02),
                        np.arange(y_min,y_max,0.02))
    z=model.predict(np.c_[xx.ravel(),yy.ravel()])#ravel 将多维数据转一维
    z=z.reshape(xx.shape)

    cs=plt.contourf(xx,yy,z)

    plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
    plt.show()

x_train,x_test,y_train,y_test=train_test_split(x_data,y_data)

dtree=tree.DecisionTreeClassifier(max_depth=4)#设置最大深度为4
dtree.fit(x_train,y_train)
plot(dtree)
dtree.score(x_test,y_test)

​

​

0.792

#Adaboost
adaboost_tree=AdaBoostClassifier(dtree,n_estimators=10)
adaboost_tree.fit(x_train,y_train)
plot(adaboost_tree)
adaboost_tree.score(x_test,y_test)

0.932

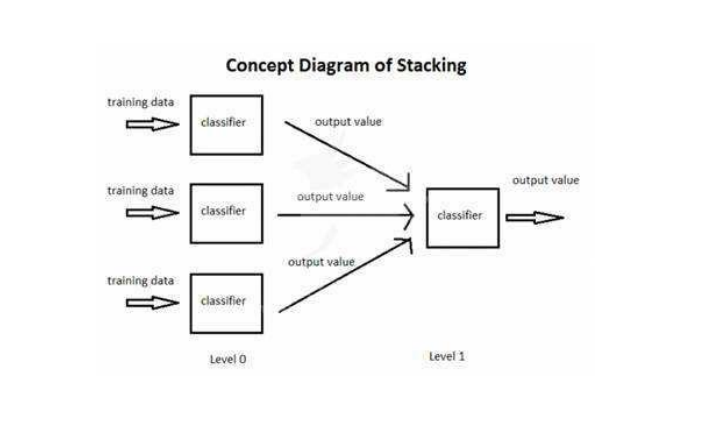
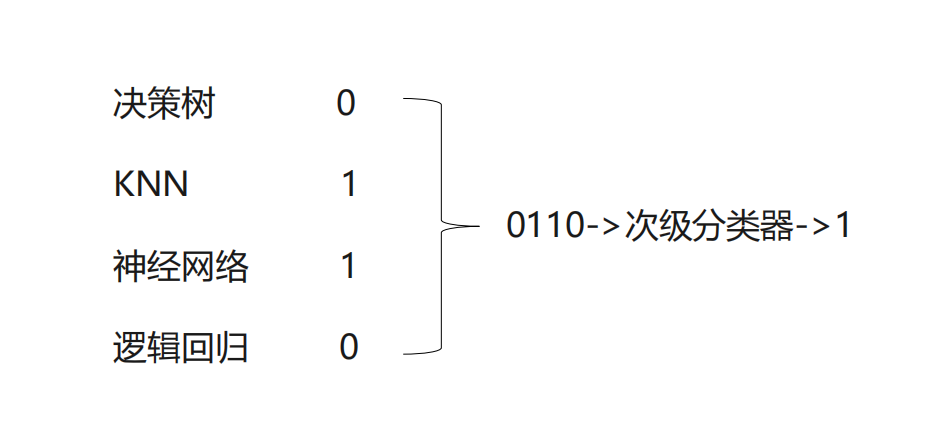
5.Stacking

stacking使用多个不同的分类器对训练集进行预测，把预测得到的结果作为一个次级分类器的输入。次级分类器的输出是整个模型的预测结果。

下面用4个不同的模型得到了不同的结果，将输出的结果组合起来在输入到次级分类器中，训练次级分类器来得到最终输出。

from sklearn import datasets
from sklearn import model_selection#交叉验证
from sklearn.linear_model import LogisticRegression#逻辑回归
from sklearn import neighbors
from sklearn import tree
from mlxtend.classifier import StackingClassifier#stack

iris=datasets.load_iris()
#只用两个特征
x_data=iris.data[:,1:3]
y_data=iris.target

#定义3个不同的分类器
clf1=neighbors.KNeighborsClassifier(n_neighbors=1)
clf2=tree.DecisionTreeClassifier()
clf3=LogisticRegression()

#定义一个次级分类器 使用逻辑回归作为次级分类器
lr=LogisticRegression()
sclf=StackingClassifier(classifiers=[clf1,clf2,clf3],meta_classifier=lr)

for clf,label in zip([clf1,clf2,clf3,sclf],
                    ['KNN','Tree','logiitic','Stack']  ):
    
    scores=model_selection.cross_val_score(clf,x_data,y_data,cv=3,scoring='accuracy')
    print(scores.mean(),label)

0.9066666666666667 KNN
0.9133333333333334 Tree
0.9533333333333333 logiitic
0.9333333333333332 Stack

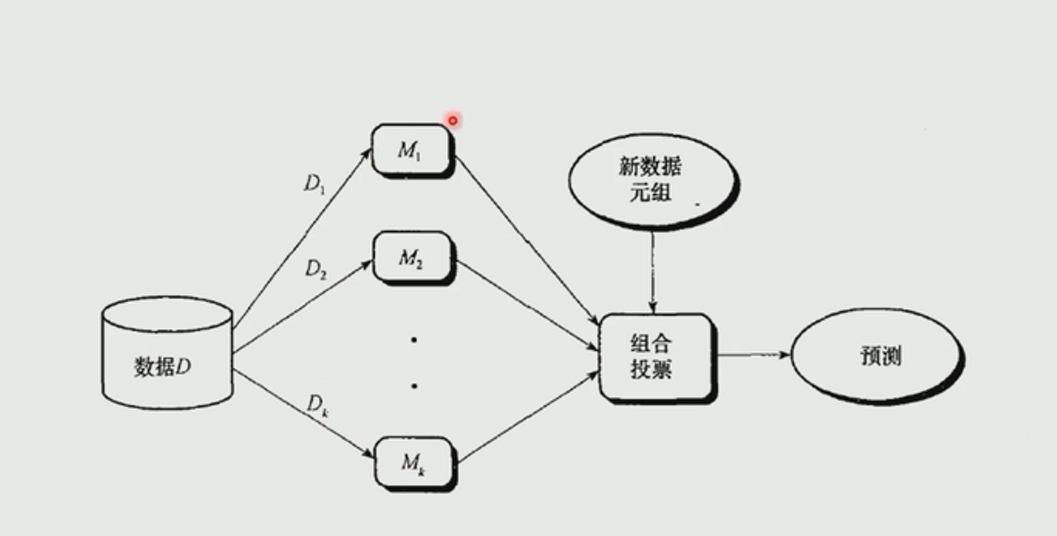
投票
投票与Stack类似但不同的是Stack会有一个次级分类器通过继续训练次级分类器来通过次级分类器来得到最终结果。
投票则没有次级分类器，直接对个模型计算出的结果进行投票，票数多者即为最终结果

from sklearn.ensemble import VotingClassifier

iris=datasets.load_iris()
#只用两个特征
x_data=iris.data[:,1:3]
y_data=iris.target

#定义3个不同的分类器
clf1=neighbors.KNeighborsClassifier(n_neighbors=1)
clf2=tree.DecisionTreeClassifier()
clf3=LogisticRegression()

#投票
sclf=VotingClassifier([('knn',clf1),('tree',clf2),('logic',clf3)])


for clf,label in zip([clf1,clf2,clf3,sclf],
                    ['KNN','Tree','logiitic','voting']  ):
    
    scores=model_selection.cross_val_score(clf,x_data,y_data,cv=3,scoring='accuracy')
    print(scores.mean(),label)

0.9066666666666667 KNN
0.9133333333333334 Tree
0.9533333333333333 logiitic
0.9333333333333332 voting