生成模型

生成模型：给定训练集，产生与训练集同分布的新样本。即如下图所示希望学到一个模型$p_{model}(x)$,其训练样本的分布$p_{data}(x)$相近。假设我们给定了一万张二次元头像的图片，通过对这一万张图片学习之后得到的模型知道如何这些图片是如何产生的，并且可以生成出与新的二次元图片，并与原来的图片是同一类的(即同分布)。但我们的原来的图片的特征空间的分布我们是不知道的，我们的目标就是寻找一个与其同概率密度函数的模型，从该模型从去采样得到的样本就是我们想要生成的图片。

所以这里就是无监督学习里面的问题:密度估计问题。其主要学习思路主要有两类：

• 一类是显示的密度估计：显示的定义并求解分布$p_{model}(x)$，主要有PixelRNN/PixelCNN和VAE。
• 另一类是隐式的密度估计：学习一个模型$P_{model}(x)$，而无需定义它。主要有GAN，GSN。

PixelRNN与PixelCNN

PixelRNN

这是一个显示的密度模型。其思路为利用链式准则将图像x的生成概率转变为每个像素生成的概率的乘积，其学习过程就是最大化训练数据的似然。

$$p_{x}=\prod_{i=1}^{n}p(x_{i}|x_{1},...,x_{i-1} )$$

$p_{x}$是图片x的似然，在给定已经生成的像素前提下生成第i个像素的概率。
PixelRNN就是一张图片看成了一段序列，先生成第一个像素点的值，再在第一个值的基础上生成第二个值(即求出0-255每个像素对应的概率，取最大值)，再再第一二个点的基础上生成第三个点。
我们也看到了，PixelRNN要按序列产生图像，其每一张图像都是从左上角开始产生像素的，要得到后面的像素点必然要等待前面的像素产生完毕，所以通过序列产生整张图片太慢了。其在训练过程中也是如此，所以后来改进出了PixCNN。

PixelCNN

PixCNN依然是从图像左上角来产生像素，也是基于已生成的像素，利用CNN来生成新的像素。

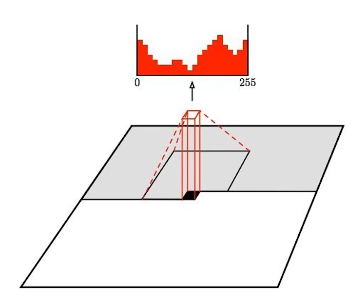
其主要运算过程如上图所示，其中灰色部分是我们已生成的像素，黑色像素点是我们待生成的点，我们我们使用256个卷积核对该像素点周围的以生成的像素点做卷积运算（即图中灰色部分），其周围未生成的像素点不参与运算，再将输出通过Softmax得到输出。
由于上下文信息已知，PixelCNN再训练的时候可以进行并行卷积，其训练速度会比PixelRNN快，但是其产生图像的过程还是逐像素的序列生成，速度依然很慢。

PixelRNN与PixelCNN的优点是他的似然函数可以精确的计算，其产生图片的过程是通过计算每个像素点的概率来获得的；此外利用似然函数的值可以有效的评估模型性能。其缺点是产出序列的速度太慢。

VAE(Variation Autoencoders)

自编码器(Auto-Encoder)

推荐文章(主要看代码部分来理解网络结构)
自编码器是一种无监督式学习模型，主要用来特征学习，其目标是利用无标签数据找到一个有效的低维的特征提取器。其主要结构如图所示：其主要包含两个部分，Encoder(编码器)和Decoder(解码器)。解码器的主要作用是把高维的X编码成低维的隐变量z；而解码器的作用是把隐藏变量h还原到初始维度。

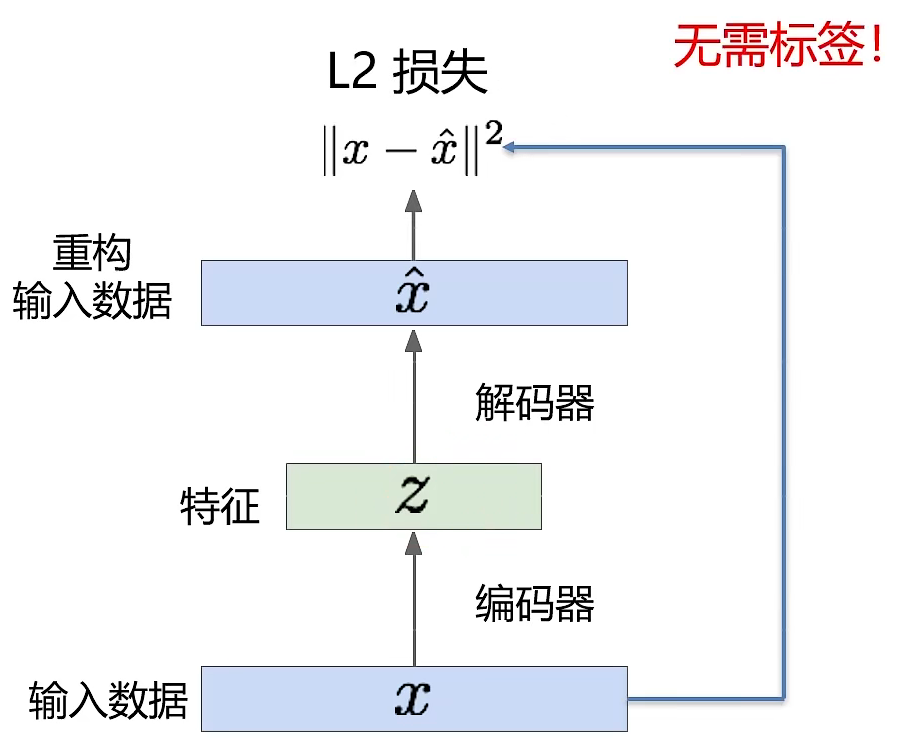
我们通过编码器来获得输入x的主要特征，由于没有正确的z，所以仅有编码器是无法对模型进行训练的，所以这时候就需要解码器，解码器通过编码z来生成一个新的x，我们希望这个x与我们的输入x越接近越来，由此得到了我们的代价函数$(x-\hat{x})^{2}$.
那么这个编码器有什么用呢？在少样本的情况下，我们可以用已经训练好的自编码器去掉解码器部分，将解码器作为有监督学习的初始特征提取模型，在提取出来的主要特征后面借一个全连接层来进行分类等任务，将最后的输入$\hat{y}$与真实值y进行比较，如果还有差距，我们可以对编码器的参数进行微调。但目前效果仍然还是不太理想。

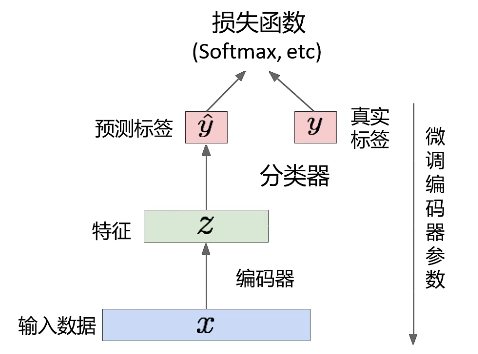
而我们的解码器则可以通过给定一个编码来生成其对应的图片或样本来进行采样工作。

变分自编码器（VAE）

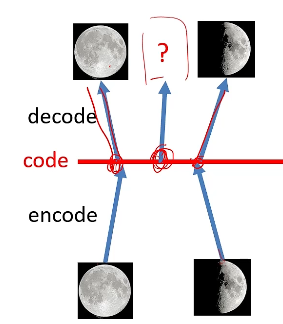
首先，我们来说明我们为什么需要VAE，我们首先来看下面这张图片，图中的，我们用半月和满月来训练我们的自编码器，但是我们希望给定半月和满月对于的编码的中间值来给到解码器，给我们输入一个3/4的月亮，但是对于自编码器来说，由于其在训练过程中并没有3/4的月亮，所以我们想要让其生成3/4的月亮也是强人所难的，这是就需要用到了我们的变自分编码器。

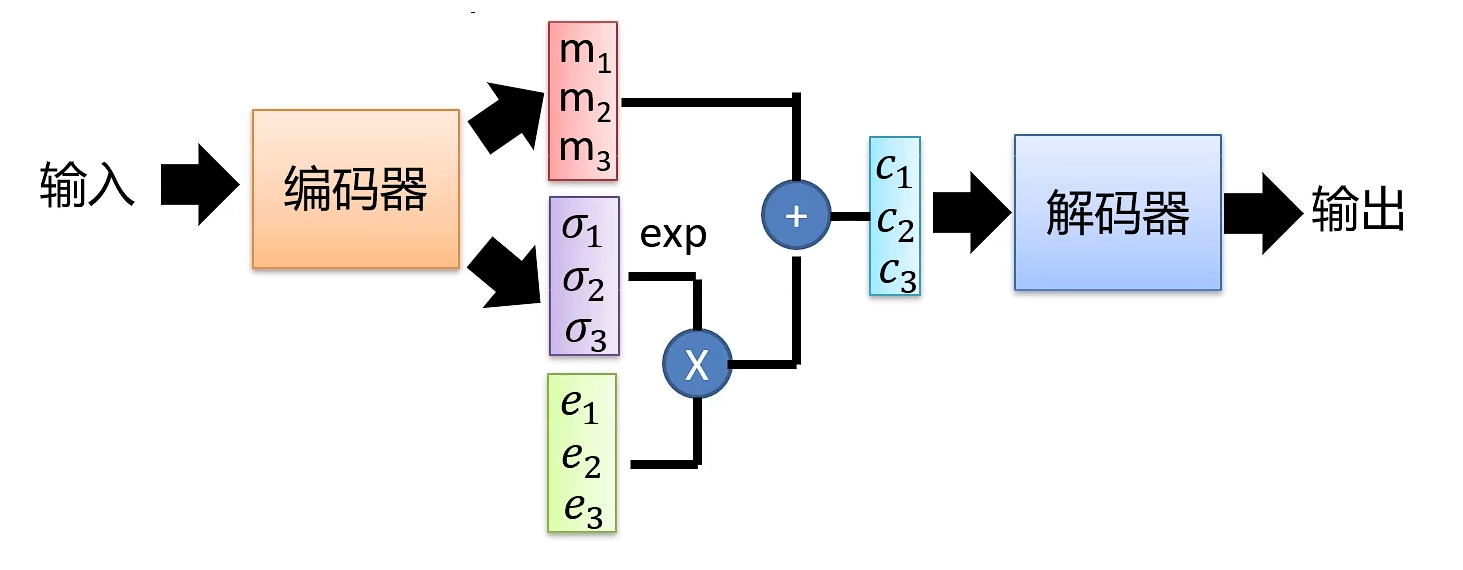
变自分编码器的结构如图所示，其主要思想是先通过输入x学习到一个分布，再在x的的分布中采样出一个z到解码器中来生成数据。其中m是x的分布的均值，$\sigma$是x的分布的标准差，(m和$\sigma均通过全连接层学习得到$)e是采样的倍率。$c_{i}=exp(\sigma_{i})*e_{i}+m_{i}$.该式子是说VAE并不是像自编码器那样直接将编码器提取出来的特征编码直接输入到解码器中，而是再给他加上一个噪声(即$exp(\sigma_{i})*e_{i}$)，来采样出一个新的特征编码。

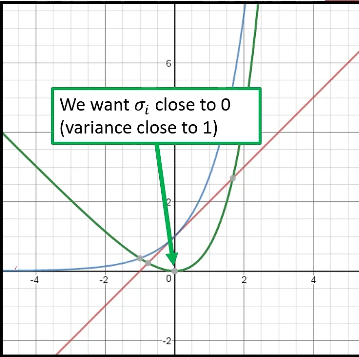
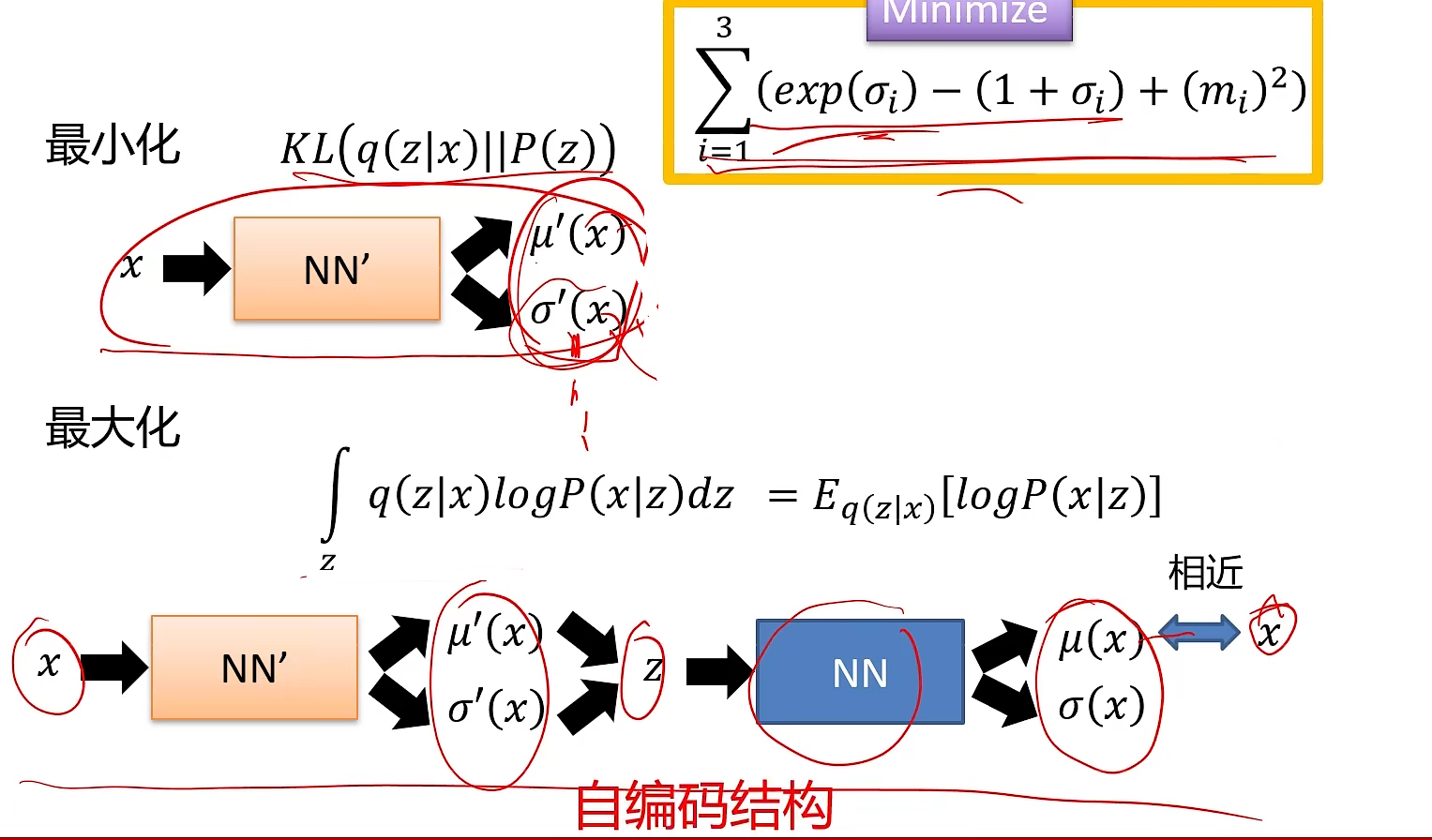
那么我们的代价函数是如何呢？如果我们像自编码器那样，只通过$(x-\hat{x})^{2}$来评估模型的话，那么我们的网络中的$\sigma$就不会进行训练(全部学成了0)，我们的网络就变成了自编码器。所以我们就需要另外一个代价函数$\sum_{i=1}(exp(\sigma_{i})-(1+\sigma_{i})+m_{i}^{2})$，其中$exp(\sigma_{i})-(1+\sigma_{i})$的图像如下图绿色曲线所示，我们希望这个式子最小，那么此时$\sigma$就越接近与0，$exp(\sigma)$就越接近与1，即希望我们的特征编码符合正态分布。$m^{2}$则是L2正则化，我们希望我们取出来的z能够分散开来。
。

变分自编码器推导

我们先来介绍一下高斯混合模型，一个高斯混合模型可以看作是有m可高斯模型混合而成的模型，每个子模型被称为一个高斯组件。

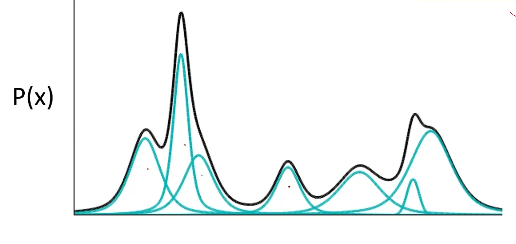
高斯混合模型的概率分布为：

$$P(x)=\sum_{m}P(m)P(x|m)$$

p(m)是选到第m个高斯组件的概率。
我们假设我们的特征向量z服从正太分布，我们再正态分布中去采样出一个z，我们用采样出的这个z去生成一个高斯组件(通过神经网络来学习)，这样我们就能生成许多个高斯组件，进而用着些高斯组件去组成一个高斯混合模型来逼近我们的输入x的真实分布。
所以我们此时就需要求x的概率的最大似然即$L=\sum(x)^{z}log(p(x))$.此时$p(x)=\int_{z}p(z)p(x|z)$
我们已知P(z)是正态分布，x|z 符合$N(u(z),\sigma(z))$，其中u(z),$\sigma(z)$为带估计的参数。由于我们的z是一个隐含量,所以我们并不能直接的求出最大化的L。所以我们需要另一个分布q(z|x),其中$z|x~N(u^{,}(x),\sigma^{,}(x))$,(同样用神经网络来学习)

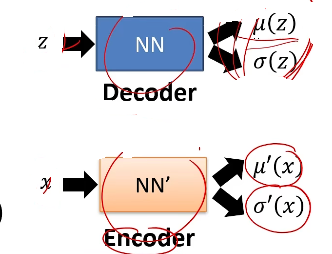
所以我们的L变为:
$logP(x)=\int_{z}q({z|x})logP(x)dz$,因为$\int_{z}q(z|x)dz=1$
,接下来的计算如图所示：其中KL是KL散度,用来度量两个分布之间的距离，其常见形式为：

$$D_{KL}(p||q)=\sum_{i=1}^{N}p(x_{i})log\frac{p(x_{i})}{q(x_{i})}$$

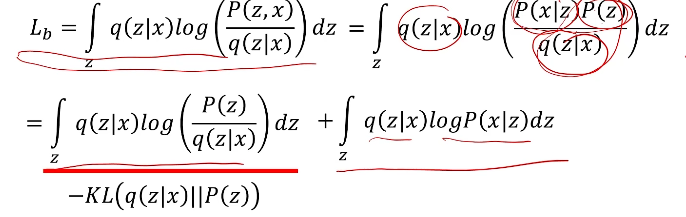
我们来看最终结果的前一部分，它是一个负的KL散度，要想使我们的L最大，那么该KL散度应该越小，即趋于0，而我们的P(z)是一个正态分布，那么q(z|x)也应该服从于正太分布(解释了前面第二个代价函数最小化$\sigma$为什么要趋于0)对应了我们的第二个代价函数.第二部分是我们给定一个x产生一个z，并利用这个z再生成一个$\hat{x}$,此时其概率越大，那么就说明此时$\hat{x}$与x就越像，那么就对应了$(x-\hat{x})^{2}$应越小越好。

生成对抗网络(GAN)

生成对抗网络的网络结构由生成网络和判别网络两部分组成。生成网络的作用是期望能够产生尽量真实的图片，进而去骗过判别器，而判别网络则是期望能够准确的区分真假图片。
其整个训练过程相当于造假钞团伙与警察的博弈过程，生成网络希望能够造出骗过警察的假钞而不断提高自己的造假技术，而警察则是希望能够更加准确的鉴定出假钞也在提升自己的鉴定技术。GAN就是在生成网络和判别网络的博弈中训练出来的。
GAN采用minmax的方式联合训练，其表达式为：

$$min_{\theta_{g}}max_{\theta_{d}}[E_{x~p_{data}}logD_{\theta_{d}}(x)+E_{z~p_{z}}log(1-D_{\theta_{d}}(G_{\theta_{g}}(z)))]$$

其中$p_{data}$是真实数据的分布，$p_{z}$是生成的图片的分布，$G_{\theta_{g}}(z)))$是生成的样本，$D_{\theta_{d}}(x)$是判别器对真是样本x的打分，$D_{\theta_{d}}(G_{\theta_{g}}(z))$是判别器对生成样本$G_{z}$的打分，打分均在(0,1)之内。
判别器$\theta_{d}$希望最大化目标函数使得$D(x)$(真是样本)接近于1，而$D(G(z))$(假样本)接近于0.生成器$\theta_{g}$希望最小化目标函数使得$D(G(z))$尽量接近于1，即希望判别器认为生成器产生的图像G(z)为真是图像。
其训练过程是交替完成的：

1. 先采用梯度上升来训练判别器：

$$max_{\theta_{d}}[E_{x~p_{data}}logD_{\theta_{d}}(x)+E_{z~p_{z}}log(1-D_{\theta_{d}}(G_{\theta_{g}}(z)))]$$

2. 在采用梯度下降来训练生成器：

$$min_{\theta_{g}}[E_{z~p_{z}}log(1-D_{\theta_{d}}(G_{\theta_{g}}(z)))]$$

但是在训练生成器的时候，直接优化这个目标函数并不是很有效。应为$log(1-D_{\theta_{d}}(G_{\theta_{g}}(z)))$的函数图像如下图所示，当生成器生成的样本效果很差时，判别器输出值会很小，此时生成器的损失函数在此处得到的梯度会很小，使得生成器学习的非常慢。相反，当生成器生成的样本较好时，判别器输出值会较大，此时生成器的损失函数在此处得到的梯度又会很大，生成器更新较快。

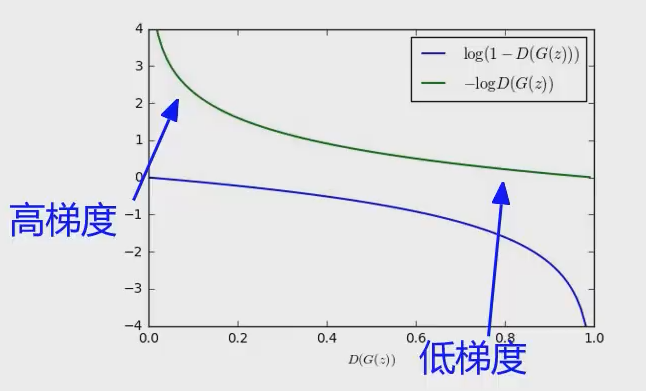
所以我们采用下面这种目标函数进行训练:

$$max_{\theta_{g}}[E_{z~p_{z}}log(D_{\theta_{d}}(G_{\theta_{g}}(z)))]$$