K近邻算法(kNN) | 忘生的blog

1.k近邻算法

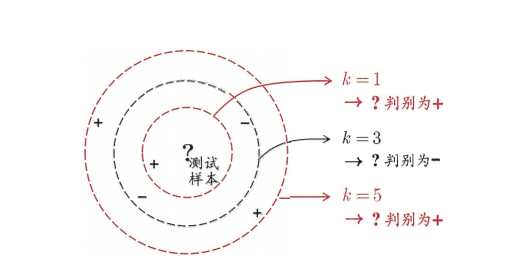
k近邻学习(K-Nearest Neighbor,简称KNN)学习是一种常用的监督学习方法，其工作机制非常简单：给定测试样本，基于某种距离度量找出训练集中与其距离最近的k个样本，然后通过这k个邻居样本来进行预测，那种类别的邻居数量多，这个测试样本就被认为是那个类别的。与“投票”较为类似。下图是一个KNN的二分类问题的一个实列，可以看出k的取值不同，测试样本的分类也会不同，但都是基于他的邻居的投票的出的。

下面给出KNN算法的步骤：

① 计算未知样本与所有已知样本实列的距离。

②对距离从小到大进行排序

③选择出最近的k个已知实列

④这k个实列邻居进行投票，哪一个类别的票数多就认为k是那个类别的

其中计算的距离一般为欧氏距离(欧几里得距离)：

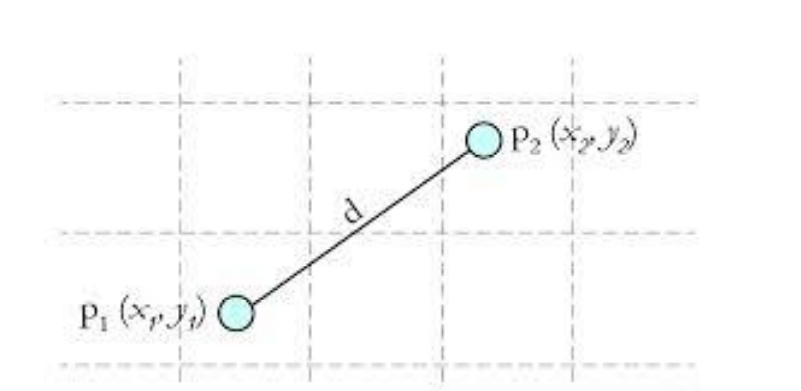
如图所示的欧几里得距离为： $\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$ 。
算法的缺点为：①算法复杂度较高，需要计算所有已知样本与要分类样本的距离。

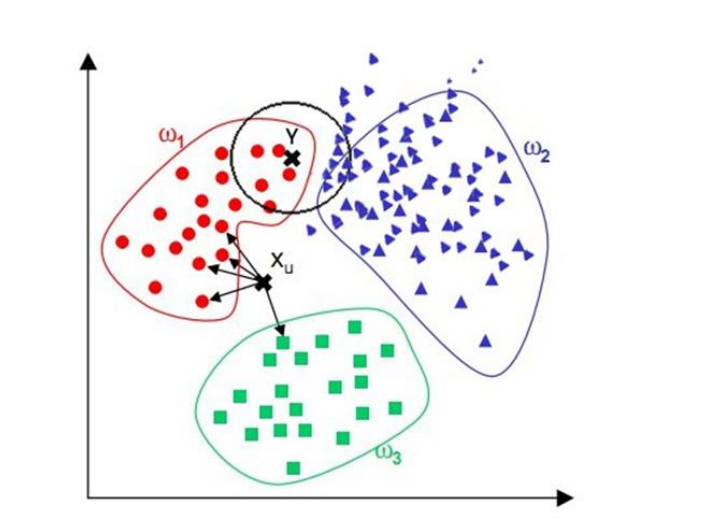
②当样本分布不平衡时，比如其中一类样本过大（实列数量过多）占主导时，新的未知实列容易被归类为这个主导样本，应为这类样本实列实列的数量过大，但这个新的未知实列实际并没有接近目标样本。如下图所示的黑色未知样本点，由于紫色的样本分布比红色样本分布更加密集，所以在分类时很容易将该未知样本分为了紫色类别，而通过观察显然应该被分为红色类别才合理一些。

2.代码实现

import numpy as np
import operator
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn import datasets

手工实现

def knn(x_test,x_train,y_train,k):
    distance=((np.tile(x_test,(x_train.shape[0],1))-x_train)**2).sum(axis=1)**0.5
    #np.title(x,(y,1))表示对x的行复制y次，列复制1次
    #sum(axis=1)表示对行求和
    #求所要预测点到所有样本点的欧式距离
    sortdis=distance.argsort()#对求得的距离进行排序
    classCount={}
    #求最近的n个点不同标签的次数
    for i in range(k):
        label=y_train[sortdis[i]]

        classCount[label]=classCount.get(label,0)+1
    #对标签出现次数从大到小进行排序
    sortClass=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    
    return sortClass[0][0]

iris=datasets.load_iris()

x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target)
print(x_train.shape,x_test.shape)

(112, 4) (38, 4)

predictinos=[]

for i in range(x_test.shape[0]):
    predictinos.append(knn(x_test[i],x_train,y_train,5))
print(classification_report(y_test,predictinos))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        11
           1       0.91      0.91      0.91        11
           2       0.94      0.94      0.94        16

    accuracy                           0.95        38
   macro avg       0.95      0.95      0.95        38
weighted avg       0.95      0.95      0.95        38

sklearn 实现

from sklearn.neighbors import KNeighborsClassifier
model=KNeighborsClassifier()#训练模型
model.fit(x_train,y_train)
predictinos1=model.predict(x_test)#预测结果
print(classification_report(y_test,predictinos1))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        11
           1       0.91      0.91      0.91        11
           2       0.94      0.94      0.94        16

    accuracy                           0.95        38
   macro avg       0.95      0.95      0.95        38
weighted avg       0.95      0.95      0.95        38

3.距离度量

1.距离公式的基本性质

在机器学习中，对应函数dist(),，若它是⼀"距离度量" (distance measure)，则需满⾜⼀些基本性质:

• 非负性： $dist(x_{i},y_{i})>=0$

• 同一性： $dist(x_{i},y_{i})>=0，当且仅当x_{}i=y_{i}$

• 对称性： $dist(x_{i},y_{i})=dist(y_{i},x_{i})$

• 直递性： $dist(x_{i},y_{i})<=dist(x_{i},y_{i})+dist(y_{i},z_{i})$ (三角不等式)

2.常见距离公式

①欧式距离

二维平面上点a( $x_{1},y_{1}$ )与点b( $x_{2},y_{2}$ )间的欧式距离为：

$d=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$

三维平面上点a( $x_{1},y_{1},z_{1}$ )与点b( $x_{2},y_{2},z_{2}$ )间的欧式距离为：

$d=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}}$

n维平面上点a( $x_{11},x_{12},...,x_{1n}$ )与点b( $x_{21},x_{22},...,x_{2n}$ )间的欧式距离为：

$d=\sqrt{\sum_{k=1}^{n}(x_{1k}-x_{2k})^{2}}$

②曼哈顿距离

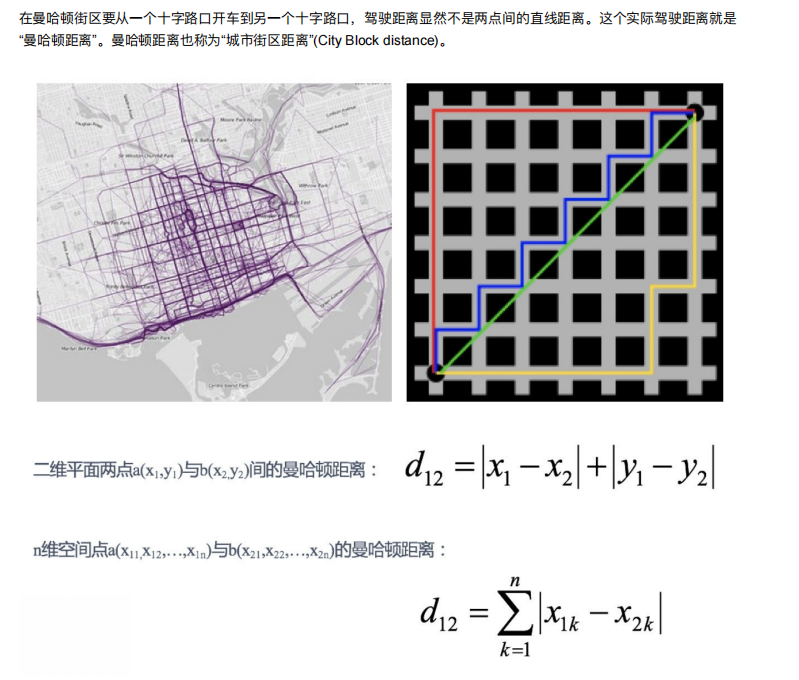
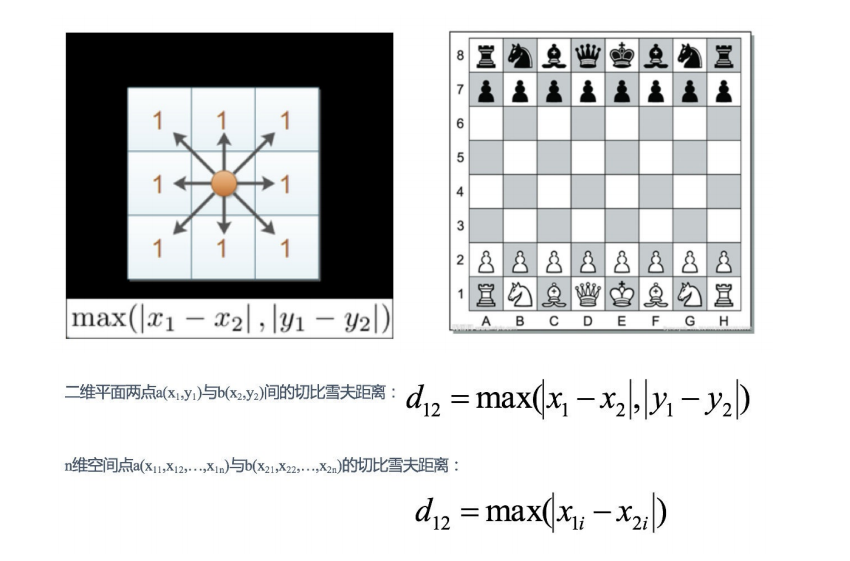
③切比雪夫距离

国际象棋中，国王可以直⾏、横⾏、斜⾏，所以国王⾛⼀步可以移动到相邻8个⽅格中的任意⼀个。国王从格⼦(x1,y1) ⾛到格⼦(x2,y2)最少需要多少步？这个距离就叫切⽐雪夫距离。

④闵可夫斯基距离

根据p的不同，闵⽒距离可以表示某⼀类/种的距离。

⼩结：

1 闵⽒距离，包括曼哈顿距离、欧⽒距离和切⽐雪夫距离，都存在明显的缺点:

e.g. ⼆维样本(身⾼[单位:cm],体重[单位:kg]),现有三个样本：a(180,50)，b(190,50)，c(180,60)。

a与b的闵⽒距离（⽆论是曼哈顿距离、欧⽒距离或切⽐雪夫距离）等于a与c的闵⽒距离。但实际上身⾼的10cm并不能

和体重的10kg划等号。

2 闵⽒距离的缺点：

(1)将各个分量的量纲(scale)，也就是“单位”相同的看待了;

(2)未考虑各个分量的分布（期望，⽅差等）可能是不同的

3.连续属性和离散数学的距离计算

我们常将属性划分为"连续属性" (continuous attribute)和"离散属性" (categorical attribute)，前者在定义域上有⽆穷多个可能的取值，后者在定义域上是有限个取值.

若属性值之间存在序关系，则可以将其转化为连续值，例如：身⾼属性“⾼”“中等”“矮”，可转化为{1, 0.5, 0}。

闵可夫斯基距离可以⽤于有序属性。

若属性值之间不存在序关系，则通常将其转化为向量的形式，例如：性别属性“男”“⼥”，可转化为{(1,0),(0,1)}