感知机

1.感知机模型

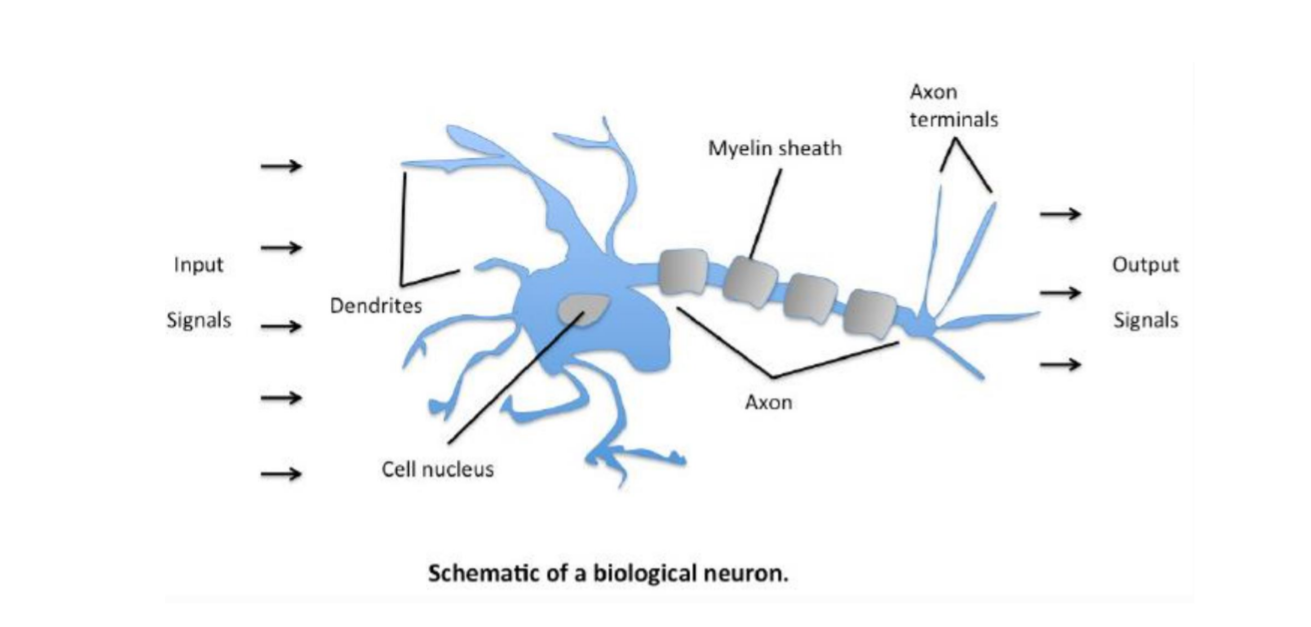
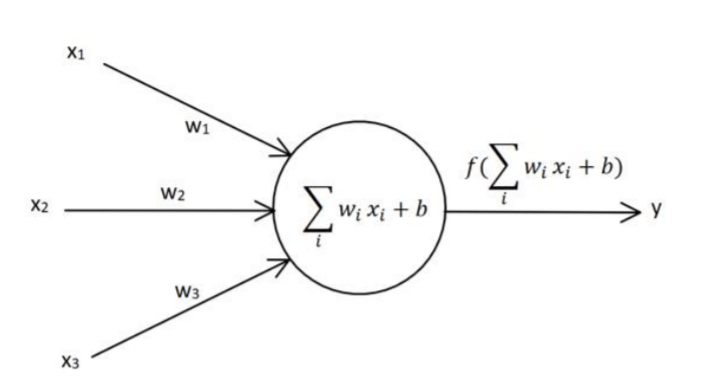
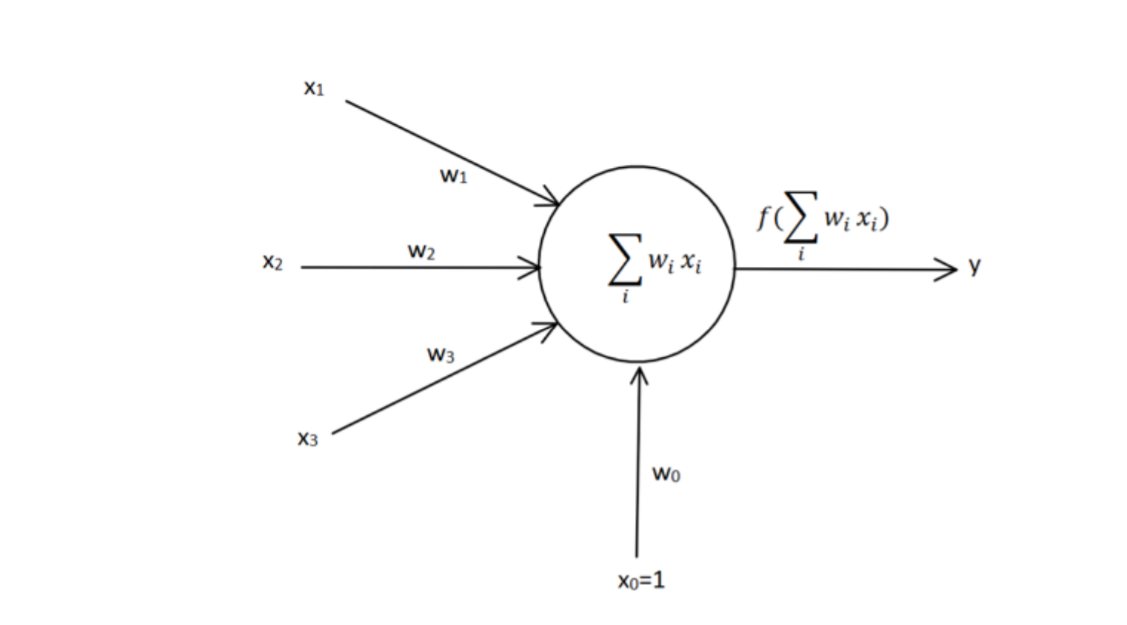
在这里插入图片描述
如图为人体神经网络图，输入信号从树突传入，在细胞核处汇总，输出信号从轴突处传出传入其他神经元，从而构成了一个人体的神经网络。而感知机其类似于一个神经元。

在这里插入图片描述

一个单层感知机与人体神经元类似，x1，x2,x3x_{1}，x_{2},x_{3}为输入结点，及神经元的输入信号，w1,w2,w3w_{1},w_{2},w_{3}为各输入结点的权重，可以理解为神经元各个树突的电阻，到达细胞核后通过进行汇总，通过一个激活函数处理后进行输出。其中，w和b称为感知机模型参数，w 叫做权重，b叫做偏置，f为激活函数，其表达式为：

sign(x)={1,x>=0−1,x<0(1)sign(x)= \begin{cases} 1,x>=0\\ -1, x<0 \end{cases} \tag{1}

在这里插入图片描述
为了方便矩阵运算，将添加一个输入恒为1的输入信号x_{0},其对应的权重w_{0}即为偏置项b。多个感知机组合起来就构成了神经网络。
 从感知机的激活函数的输出来看，感知机可以处理过后的输入信号进行分类。输出为1是一类，输出为-1又是一类。从几何上来看，感知机学习的目标是对一个线性可分得数据集T求得一个能对T中的正负样本进行正确划分的一个超平面，参数w即为该超平面的法向量，偏置b为超平面的截距。这个超平面将数据集划分为两个部分，位于平面两部分的点被分成了正负两类。

2.感知机的学习策略

 对于误分类的样本数据(x,y)来说，(y^−y)(wx+b)>0(\hat{y}-y)(wx+b)>0恒成立。应为当wx+b>=0wx+b>=0时，模型输出值为1，而样本实际值为-1，反之，当wx+b<0wx+b<0时，模型输出为-1，而实际值为1，将两种情况带入可以得到(y^−y)(wx+b)>0(\hat{y}-y)(wx+b)>0恒成立。由此，对于给定数据集T，其损失函数可定义为

L(w,b)=∑xi∈M(yi^−yi)(wxi+b)L(w,b)=\sum_{x_{i}∈M}{(\hat{y_{i}}-y_{i})}(wx_{i}+b)

M为误分类点集合
x显然损失函数是非负的，如果没有误分类点，损失函数值是0.误分类点越少，损失函数就越小。
则要求参数w,b,就可以通过求解损失函数最小值点来得出参数。故而最小化问题进一步转化为：

minwL(w)=minw∑x∈M(yi^−yi)wximin_{w}L(w)=min_{w}\sum_{x∈M}{(\hat{y_{i}}-y_{i})wx_{i}}

3.感知机的学习算法

感知机学习算法是由误分类驱动的，具体采用随梯度下降法。首先，任意选取一个超平面w0b0w_{0}b_{0},然后采用梯度下降法不断地极小化代价函数。极小化的过程不是一次使M中所有的误分类点的梯度下降，而是随机选取一个误差分类点使其梯度下降。
假设误分类样本集合M固定时，那么可以求得损失函数的梯度为：$$L(w)=\sum_{x_{i}∈M}({\hat{y_{i}}-y_{i}})x_{i}$$
通过梯度下降w法梯度更新公式为：

w=w−α(yi^−yi)xi=w+α(yi−y^)xiw=w-\alpha (\hat{y_{i}}-y_{i})x_{i}=w+\alpha{(y_{i}-\hat{y})x_{i}}

所以感知机的学习算法为：
①选取初值w0w_{0}
②在数据集中选取(x0,y0)(x_{0},y_{0})
③如果(yi−yi^)（xiw+b)<=0(y_{i}-\hat{y_i})（x_{i}w+b)<=0则w=w+Δww=w+\Delta w
④转置②，直至训练集没有误分类点

4.代码实现

1
2
3
import numpy as np
import matplotlib.pyplot as plt
import random
1
2
3
4
5
6
7
8
9
10
11
12
x=np.array([[1,3,3],
            [1,4,3],
            [1,1,1],
            [1,0,2]])
y=np.array([[1],
            [1],
            [-1],
            [-1]])
w=np.random.random([3,1])#生成一个3行1列的矩阵
lr=0.01#学习率
epochs=100#最大迭代次数
O=0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def plot():
    #正样本
    x1 = [3,4]
    y1 = [3,3]
    #负样本
    x2 = [1,0]
    y2 = [1,2]

    #计算分界线的斜率以及截距
    k = -w[1]/w[2]
    d = -w[0]/w[2]   #w0+w1*x+w2*y=0
    print('k=',k)
    print('d=',d)

    xdata=(0,5)

    plt.plot(xdata,xdata*k+d,'r')
    plt.scatter(x1,y1,c='b')
    plt.scatter(x2,y2,c='y')
    plt.show()

Δw=−α(yi^−yi)xi=α(yi−yi^)xi\Delta{}w=-\alpha(\hat{y_{i}}-y_{i})x_{i}=\alpha(y_{i}-\hat{y_{i}})x_{i}

w=w+Δww=w+\Delta w 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def gard():
    global x,y,lr,w
    O=np.sign(np.dot(x,w))#预测输出
    #print(O)
    for i in range(x.shape[0]):
        a=x[i,:,np.newaxis].reshape(1,-1)
        b=O[i,:,np.newaxis].reshape(1,-1)
        if(np.dot(a,w)[0,0]*(y[i]-b)[0,0]<0):
            a=x[i,:,np.newaxis].reshape(1,-1)
            b=O[i,:,np.newaxis].reshape(1,-1)
            w_c=a.T.dot(y[i]-b)#
            w=w+lr*w_c#更新梯度
            break
    #print(w)
    return w
w=np.random.random([3,1])#生成一个3行1列的矩阵
for i in range(5000):
    w=gard()
    O=np.sign(np.dot(x,w))
    if(O==y).all():
        #print(O)
        #print(i)
    # if(i%10==0):
    #     plot()
    #     #print(w)
    #     #print(O)
        break  
plot()  
k= [-0.09968292]
d= [2.60720738]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-290Grk3T-1642044127399)(output_5_1.png)]

BP神经网络

感知机虽然可以很好的解决线性二分类问题，但是却无法解决非线性的分类问题，甚至连异或这样最简单的的非线性可分的问题。所以便提出了神经网络。

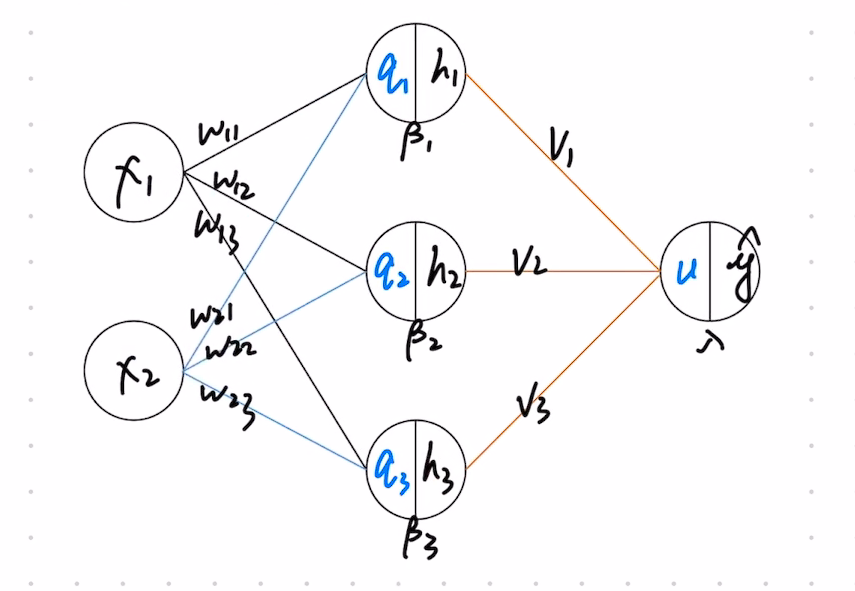
BP神经网络结构


上图是一个简单的两层神经网络。其中x1,x2x_{1},x_{2}这一层叫做输入层，中间的一层叫做隐藏层，最右边的那层叫做输出层。对于一个神经网络来言，输入层和输出层只有一个，隐藏层可以有很多层。
在该神经网络中，q，u是上一层经过线性运算后经过激活函数的结果，h，y是经过激活函数后的输出。其中

qi=x1w1i+x2i+x3i+βiq_{i}=x_{1}w_{1i}+x_{2i}+x_{3i}+\beta_{i}

hi=f(qi),f为激活函数h_{i}=f(q_{i}) ,f为激活函数

u(h1v1+h2v2+h3v3+λ)u(h_{1}v_{1}+h_{2}v_{2}+h_{3}v_{3}+\lambda)

y^=f(u),f为激活函数\hat{y}=f(u),f为激活函数

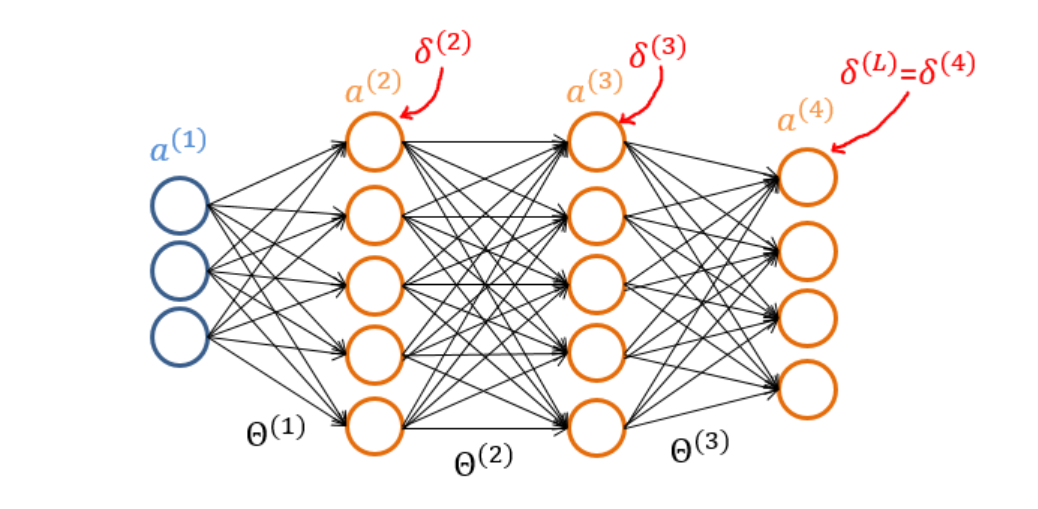
BP神经网络的训练

对于BP神经网络，我们采用反向传播算法来求解参数，训练模型。
反向传播算法的思路如下：给定一个样例(x,y)，我们首先进行"前向传播"运算，计算出网络中所有的激活值和每层神经元经过线性变换后算出的未经激活函数前的值。之和，针对第l层的每一个节点i，我们计算出其残差δ\delta,该残差表明了该节点对最终输出值的残差产生的多少影响。
反向传播算法的步骤为：
①进行前向传播，计算出每一层神经元的值
②对于输出层(第$$n_{l}$$层)：
计算δ(nl)=(a(nl)−y)′(z(nl))\delta^{(n_{l})}=(a^{(n_{l})}-y)^{'}(z^{(n_{l})})
③对于第n=l-1，l-2,l-3,…,2的各层，
计算：δ(l)=(θ(l))Tδ(l+1)⋅∗f′(z(l))\delta^{(l)}=(\theta^{(l)})^{T}\delta^{(l+1)}·*f^{'}(z^{(l)})
④计算最终所需要的偏导数值:
∇θ(l)J=δ(l+1)(a(l))T\nabla_{\theta^{(l)}}J=\delta^{(l+1)}(a^{(l)})^{T}
∇b(l)J=δ(l+1)\nabla_{b^{(l)}}J=\delta^{(l+1)}
⑤进行梯度下降法的一次迭代：
  1.对于所有的n，令Δθ(l)=0,Δb(l)=0\Delta{\theta^{(l)}}=0,\Delta{b^{(l)}}=0
  2.对于i=1到m：（m为样本总数）
   1.利用反向传播算法计算∇θ(l)J\nabla_{\theta^{(l)}}J和∇b(l)J\nabla_{b^{(l)}}J
   2.计算Δθ(l)=Δθ(l)+∇θ(l)J\Delta{\theta^{(l)}}=\Delta{\theta^{(l)}}+\nabla_{\theta^{(l)}}J
   3.计算Δb(l)=Δb(l)+∇b(l)J\Delta{b^{(l)}}=\Delta{b^{(l)}}+\nabla_{b^{(l)}}J
  3.更新权重参数：
θ(l)=θ(l)−α1mΔθ(l)\theta^{(l)}=\theta^{(l)}-\alpha{\frac{1}{m}\Delta{\theta^{(l)}}}
b(l)=b(l)−α1mΔb(l)b^{(l)}=b^{(l)}-\alpha{\frac{1}{m}\Delta{b^{(l)}}}

反向传播算法推导

首先构造损失函数L=12(y^−y)2L=\frac{1}{2}(\hat{y}-y)^{2}$
链式求导可得：

∂L∂v=∂L∂u∂u∂v=∂L∂y^∂y^∂u∂u∂v=(h^−y)f’(u)h\frac{\partial{L}}{\partial{v}}=\frac{\partial{L}}{\partial{u}}\frac{\partial{u}}{\partial{v}}=\frac{\partial{L}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{u}}\frac{\partial{u}}{\partial{v}}=(\hat{h}-y)f^{’}(u)h

∂L∂w=∂L∂q∂q∂w=∂L∂y^∂y^∂u∂u∂h∂h∂q∂q∂w=(h^−y)f’(u)vf’(q)x\frac{\partial{L}}{\partial{w}}=\frac{\partial{L}}{\partial{q}}\frac{\partial{q}}{\partial{w}}=\frac{\partial{L}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{u}}\frac{\partial{u}}{\partial{h}}\frac{\partial{h}}{\partial{q}}\frac{\partial{q}}{\partial{w}}=(\hat{h}-y)f^{’}(u)vf^{’}(q)x

利用链式法则来计算梯度更新权重方法简单，但是计算出来的结果过于冗长。由于更新的过程可以看做是从网络的输入层到输出层从前往后更新，每次更新的时候都需要重新计算节点的误差，因此会存在一些不必要的重复计算。其实对于已经计算完毕的节点我们完全可以直接拿来用，因此我们可以重新看待这个问题，从后往前更新。先更新后边的权重，之后再在此基础上利用更新后边的权重产生的中间值来更新较靠前的参数。所有引入了中间变量δ\delta,来简化公式并且减少计算。根据上边的计算过程我们可以观察出：每次计算对于层的梯度，都要计算∂L∂(h或q)\frac{\partial{L}}{\partial{(h或q)}}，而这个h或q恰好就是为经激活函数之前的值。所有我们就令δ=∂L∂(h或q)\delta=\frac{\partial{L}}{\partial{(h或q)}},所以通过观察这个上边两个式子，我们可以得出：
∂L∂v=∂L∂u∂u∂v=δ3h,δ3=(y^−y)f’(u)\frac{\partial{L}}{\partial{v}}=\frac{\partial{L}}{\partial{u}}\frac{\partial{u}}{\partial{v}}=\delta^{3}h,\delta^{3}=(\hat{y}-y)f^{’}(u)
∂L∂w=∂L∂q∂q∂w=δ2x,δ2=(h^−y)f’(u)vf’(q)=δ3vf’(q)\frac{\partial{L}}{\partial{w}}=\frac{\partial{L}}{\partial{q}}\frac{\partial{q}}{\partial{w}}=\delta^{2}x,\delta^{2}=(\hat{h}-y)f^{’}(u)vf^{’}(q)=\delta^{3}vf^{’}(q)

是不是根据归纳出来的有些牵强，下面我们来证明这个式子：
在这里插入图片描述
假设我们的神经网络如图所示，x0:偏置，x0=1x_{0}:偏置，x_{0}=1
θ:权重\theta:权重
ai(j):代表第j层第i个激活单元a^{(j)}_{i}:代表第j层第i个激活单元
zi(j)：代表第j层第i个为未经激活函数的值，ai(j)=f(zi(j))z^{(j)}_{i}：代表第j层第i个为未经激活函数的值，a^{(j)}_{i}=f(z^{(j)}_{i})
θ(j):代表第j层到第j+1层的权重矩阵\theta^{(j)}:代表第j层到第j+1层的权重矩阵
θv,u(j):第j成的第u各到第j+1层的第v个单元的权重。\theta^{(j)}_{v,u}:第j成的第u各到第j+1层的第v个单元的权重。
如果第j层有m个单元，第j加一层有n个单元，那么θ(j)将会是一个n∗（m+1）的矩阵如果第j层有m个单元，第j加一层有n个单元，那么\theta^{(j)}将会是一个n*（m+1）的矩阵 s_{j}:$第j 层的激活单元数目，不包括偏置单元

我们的激活函数为：
J=12(y^−y)2J=\frac{1}{2}(\hat{y}-y)^{2}
令δ(j)=∂J∂z(j)\delta^{(j)}=\frac{\partial{J}}{\partial {z^{(j)}}}
对于输出层（第l层）：
δ(l)=∂J∂z(l)\delta^{(l)}=\frac{\partial{J}}{\partial {z^{(l)}}}
=∂z(l)12(y^−y)2=\frac{\partial} {z^{(l)}}\frac{1}{2}(\hat{y}-y)^{2}
=∂z(l)12(a(l)−y)2=\frac{\partial} {z^{(l)}}\frac{1}{2}(a^{(l)}-y)^{2}
=∂z(l)12(f(z(l))−y)2=\frac{\partial} {z^{(l)}}\frac{1}{2}(f(z^{(l)})-y)^{2}
=(y^−y)⋅∗f’(z(l))=(\hat{y}-y)·*f^{’}(z^{(l)})
对于第l-1层：
δ(l−1)=∂J∂z(l−1)\delta^{(l-1)}=\frac{\partial{J}}{\partial {z^{(l-1)}}}
=∂z(l−1)12(y^−y)2=\frac{\partial} {z^{(l-1)}}\frac{1}{2}(\hat{y}-y)^{2}
=∂z(l−1)12(a(l)−y)2=\frac{\partial} {z^{(l-1)}}\frac{1}{2}(a^{(l)}-y)^{2}
=∂z(l−1)12(f(zl)−y)2=\frac{\partial} {z^{(l-1)}}\frac{1}{2}(f(z^{l})-y)^{2}
=(y^−y)∂∂z(l−1)f(z(l))=(\hat{y}-y)\frac{\partial}{\partial{z^{(l-1)}}}f(z^{(l)})
=(y−y^)f′(z(l))∂z(l)∂z(l−1)=(\hat{y-y})f^{'}(z^{(l)})\frac{\partial{z^{(l)}}}{\partial{z^{(l-1)}}}
=δ(l)∂(f(z(l−1))θ(l−1))∂z(l−1)=\delta^{(l)}\frac{\partial(f(z^{(l-1)})\theta^{(l-1)})}{\partial{z^{(l-1)}}}
=δ(l)θ(l−1)f′(z(l−1))=\delta^{(l)}\theta^{(l-1)}f^{'}(z^{(l-1)})

所以：
δ(l)=δ(l+1)θ(l)⋅∗f′(z(l))\delta^{(l)}=\delta^{(l+1)}\theta^{(l)}·*f^{'}(z^{(l)})
下面我们计算偏导数：
∂Jθ(l)\frac{\partial{J}}{\theta^{(l)}}
=∂J∂zl+1∂z(l+1)∂θ(l)=\frac{\partial{J}}{\partial{z^{l+1}}}\frac{\partial{z^{(l+1)}}}{\partial{\theta^{(l)}}}
因为z(l+1)=θ(l)a(l)z^{(l+1)}=\theta^{(l)}a^{(l)}
所以∂z(l+1)∂θ(l)=a(l)\frac{\partial{z^{(l+1)}}}{\partial{\theta^{(l)}}}=a^{(l)}
∂J∂zl+1=δ(l+1)\frac{\partial{J}}{\partial{z^{l+1}}}=\delta^{(l+1)}

∂J∂θ(l)=δ(l+1)a(l)\frac{\partial{J}}{\partial{\theta^{(l)}}}=\delta^{(l+1)}a^{(l)}

对于激活函数为sigmoid函数，f′(zl)=a(l)(1−a(l))f^{'}(z^{l})=a^{(l)}(1-a^{(l)})。
证明如下：
对sigmoid函数求导：

g(z)=11+e−zg(z)=\frac{1}{1+e^{-z}}

g′(z)=e−z(1+e−z)2g^{'}(z)=\frac{e^{-z}}{(1+e^{-z})^{2}}
=11+e−ze−z1+e−z=\frac{1}{1+e^{-z}}\frac{e^{-z}}{1+e^{-z}}

=11+e−z(1+e−z1+e−z−11+e−z)=\frac{1}{1+e^{-z}}(\frac{1+e^{-z}}{1+e^{-z}}-\frac{1}{1+e^{-z}})

=g(z)(1−g(z))=g(z)(1-g(z))
如果损失函数为交叉熵，对于输出层δ(l)=aL−y\delta^{(l)}=a^{L}-y。

证明如下：

J(θ)=−1m∑i=1m[y(i)log(hθ(x(i)))+(1−y(i))log(1−(hθ(x(i))))]J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_{\theta}(x^{(i)}))+(1-y^{(i)})log(1-(h_{\theta}(x^{(i)})))]

hθ(x)=a(L)=g(z(L))h_{\theta}(x)=a^{(L)}=g(z^{(L)}),g(z)=11+e−zg(z)=\frac{1}{1+e^{-z}},带入到J中(为方便计算m=1)

J(θ)=−ylog(11+e−z)−(1−y)log(1−11+e−z)J(\theta)=-ylog(\frac{1}{1+e^{-z}})-(1-y)log(1-\frac{1}{1+e^{-z}})

=ylog(1+e−z)−(1−y)log(e−z1+e−z)=ylog(1+e^{-z})-(1-y)log(\frac{e^{-z}}{1+e^{-z}})

=ylog(1+e−z)+(1−y)log(1+ez)=ylog(1+e^{-z})+(1-y)log(1+e^{z})

δ(l)=∂∂z(l)J(θ)=∂∂z(l)(ylog(1+e−z(l))+(1−y)log(1+ez(l)))\delta^{(l)}=\frac{\partial}{\partial{z^{(l)}}}J(\theta)=\frac{\partial}{\partial{z^{(l)}}}(ylog(1+e^{-z^{(l)}})+(1-y)log(1+e^{z^{(l)}}))

=y−e−z(l)1+e−z(l)+(1−y)ez(l)1+ez(l)=y\frac{-e^{-z^(l)}}{1+e^{-z^{(l)}}}+(1-y)\frac{e^{z^{(l)}}}{1+e^{z^{(l)}}}

=−ye(−z(l))−ye−z(l)ez(l)+1−y+ez(l)−ye(zl)(1+e(−z(l)))(1+e(z(l)))=\frac{-ye^{(-z^{(l)})}-ye^{-z^{(l)}}e^{z^{(l)}}+1-y+e^{z^{(l)}}-ye^{(z^{l})}}{(1+e^{(-z^{(l)})})(1+e^{(z^{(l)})})}

=(1−y)ez(l)−(1+ez(l))yez−(l)+(1−y)(1+e(−z(l)))(1+e(z(l)))=\frac{(1-y)e^{z^{(l)}}-(1+e^{z^{(l)}})ye^{z^{-(l)}}+(1-y)}{(1+e^{(-z^{(l)})})(1+e^{(z^{(l)})})}

=(1−y)(1+e(z(l))))−(1+ez(l))yez−(l)(1+e(−z(l)))(1+e(z(l)))=\frac{(1-y)(1+e^{(z^{(l)})}))-(1+e^{z^{(l)}})ye^{z^{-(l)}}}{(1+e^{(-z^{(l)})})(1+e^{(z^{(l)})})}

=(1−y−ye−z(l))(1+e(z(l)))(1+e(−z(l)))(1+e(z(l)))=\frac{(1-y-ye^{-z^{(l)}})(1+e^{(z^{(l)})})}{(1+e^{(-z^{(l)})})(1+e^{(z^{(l)})})}

=1−y(1−e(−z(l)))(1+e(−z(l)))=\frac{1-y(1-e^{(-z^{(l)})})}{(1+e^{(-z^{(l)})})}
=11+e−z(l)−y=\frac{1}{1+e^{-z^{(l)}}}-y

=g(z(l))−y=g(z^{(l)})-y

=a(l)−y=a^{(l)}-y

即证得δl=a(l)−y\delta^{l}=a^{(l)}-y

神经网络实现手写数字识别

1
2
3
4
5
6
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
from sklearn.metrics import classification_report#评估模型准确率
from sklearn import datasets#导入数据集
from sklearn.model_selection import train_test_split#对样本进行分割
准备数据
1
2
3
4
5
6
data=datasets.load_digits()
x=data.data#样本
y=data.target#标签
print(X.shape)
y.shape

(1797, 64)
(1797,)

1
2
3
4
5
def plot_an_img(img):#画出单张图片
    fig, ax = plt.subplots(figsize=(1, 1))
    ax.matshow(img.reshape((8, 8)), cmap=matplotlib.cm.binary)
    plt.xticks(np.array([]))  # just get rid of ticks
    plt.yticks(np.array([]))
1
2
3
4
pick_one = np.random.randint(0, 1797)#打印单个图片
plot_an_img(x[pick_one, :])
plt.show()
print('this should be {}'.format(y[pick_one]))

​
png

this should be 4

1
2
3
4
5
6
7
8
9
10
11
#随机画100张图片
index=np.random.choice(np.arange(X.shape[0]),100)
samples_img=x[index,:]
tar=y[index]
for i in range(1,101):
    plt.subplot(10,10,i)
    plt.imshow(samples_img[i-1].reshape([8,8]),cmap=plt.cm.gray_r)
    plt.text(3,10,str(tar[i-1]),c='r')
    plt.xticks()
    plt.yticks()
plt.show()

png

1
2
3
X=np.concatenate((np.ones((X.shape[0],1)),X),axis=1)
print(X[:5])
print(X.shape)#添加偏置项1
[[ 1.  0.  0.  5. 13.  9.  1.  0.  0.  0.  0. 13. 15. 10. 15.  5.  0.  0.
   3. 15.  2.  0. 11.  8.  0.  0.  4. 12.  0.  0.  8.  8.  0.  0.  5.  8.
   0.  0.  9.  8.  0.  0.  4. 11.  0.  1. 12.  7.  0.  0.  2. 14.  5. 10.
  12.  0.  0.  0.  0.  6. 13. 10.  0.  0.  0.]
 [ 1.  0.  0.  0. 12. 13.  5.  0.  0.  0.  0.  0. 11. 16.  9.  0.  0.  0.
   0.  3. 15. 16.  6.  0.  0.  0.  7. 15. 16. 16.  2.  0.  0.  0.  0.  1.
  16. 16.  3.  0.  0.  0.  0.  1. 16. 16.  6.  0.  0.  0.  0.  1. 16. 16.
   6.  0.  0.  0.  0.  0. 11. 16. 10.  0.  0.]
 [ 1.  0.  0.  0.  4. 15. 12.  0.  0.  0.  0.  3. 16. 15. 14.  0.  0.  0.
   0.  8. 13.  8. 16.  0.  0.  0.  0.  1.  6. 15. 11.  0.  0.  0.  1.  8.
  13. 15.  1.  0.  0.  0.  9. 16. 16.  5.  0.  0.  0.  0.  3. 13. 16. 16.
  11.  5.  0.  0.  0.  0.  3. 11. 16.  9.  0.]
 [ 1.  0.  0.  7. 15. 13.  1.  0.  0.  0.  8. 13.  6. 15.  4.  0.  0.  0.
   2.  1. 13. 13.  0.  0.  0.  0.  0.  2. 15. 11.  1.  0.  0.  0.  0.  0.
   1. 12. 12.  1.  0.  0.  0.  0.  0.  1. 10.  8.  0.  0.  0.  8.  4.  5.
  14.  9.  0.  0.  0.  7. 13. 13.  9.  0.  0.]
 [ 1.  0.  0.  0.  1. 11.  0.  0.  0.  0.  0.  0.  7.  8.  0.  0.  0.  0.
   0.  1. 13.  6.  2.  2.  0.  0.  0.  7. 15.  0.  9.  8.  0.  0.  5. 16.
  10.  0. 16.  6.  0.  0.  4. 15. 16. 13. 16.  1.  0.  0.  0.  0.  3. 15.
  10.  0.  0.  0.  0.  0.  2. 16.  4.  0.  0.]]
(1797, 65)

1
2
3
4
5
6
from sklearn.preprocessing import OneHotEncoder
encoder=OneHotEncoder(sparse=False)
y=np.array(y).reshape([-1,1])
y_onehot=encoder.fit_transform(y)
print(y_onehot[:5])#借助one-hot把y映射成'(5000,10)'大小
y_onehot.shape
[[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]]

(1797, 10)

1
2
3
4
5
#初始化参数
theta1=np.random.random((25,65))*0.01
theta2=np.random.random(((10,26)))*0.01
print(theta1.shape)
theta2.shape
(25, 65)

(10, 26)

1
2
3
#分割数据集
x_train,x_test,y_train,y_test=train_test_split(X,y_onehot)
print(x_train.shape,y_train.shape)
(1347, 65) (1347, 10)

1
2
3
4
5
6
#激活函数
def sigmoid(X):
    return 1.0/(1+np.exp(-X))
#激活函数得导数
def dsigmoid(X):
    return np.multiply(sigmoid(X),1-sigmoid(X))
前向传播
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
parameters={'theta1':theta1,
            'theta2':theta2}
def forward_propagation(X,parameters):
    theta1=parameters['theta1']
    theta2=parameters['theta2']

    a1=X#输入层
    z2=np.dot(a1,theta1.T)#输入层经过线性变幻

    a2=np.concatenate((np.ones((a1.shape[0],1)),sigmoid(z2)),axis=1)#添加偏置
    z3=np.dot(a2,theta2.T)#隐藏层经过线性变化
    a3=sigmoid(z3)#输出层

    cache={'a1':a1,
           'z2':z2,
           'a2':a2,
           'z3':z3,
           'a3':a3
           }
    return a3,cache
a3,cache=forward_propagation(X,parameters)
a3[:2]
array([[0.52583117, 0.5281081 , 0.52749448, 0.52850773, 0.52823992,
        0.53030709, 0.53145626, 0.52662732, 0.53041953, 0.52550445],
       [0.52648372, 0.52867252, 0.52801463, 0.52926495, 0.5289496 ,
        0.53114059, 0.53228084, 0.52725707, 0.53094982, 0.52605496]])
代价函数
1
2
3
4
5
6
7
8
9
10
11
#未加正则化
def cost(X,Y,parameters):

    a3,cache=forward_propagation(X,parameters)#前向传播，计算输出结果
    m=X.shape[0]

    first=np.multiply(Y,np.log(a3))
    second=np.multiply(1-Y,np.log(1-a3))#用交叉熵作为代价函数
    J=-first-second
    return J.sum()/m
cost(X,y_onehot,parameters)
7.408890217449401

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#给代价函数加上正则项
def cost_res(X,y,parameters,lamda=1):

    theta1=parameters['theta1']
    theta2=parameters['theta2']
    j=cost(X,y,parameters)
    m=X.shape[0]

    theta1=np.array(theta1)
    theta2=np.array(theta2)
    re_theta1=((theta1[:,1:])**2).sum()/(2.0*m)#计算正则项时不需要加偏置项
    re_theta2=((theta2[:,1:])**2).sum()/(2.0*m)

    J=j+lamda*re_theta1+lamda*re_theta2
    return J
cost_res(X,y_onehot,parameters)

7.408907648511851
反向传播
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
def backward_propagate(X,y,parameters,lamda=1):
    theta1=parameters['theta1']
    theta2=parameters['theta2']
    m=X.shape[0]
    a3,cache=forward_propagation(X,parameters)#前向传播
    a1=cache['a1']
    z2=cache['z2']
    a2=cache['a2']
    z3=cache['z3']

    grad_theta1=grad_theta2=0
    for i in range(m):#计算参数梯度
        a1i=a1[i,:]
        z2i=z2[i,:]
        a2i=a2[i,:]
        z3i=z3[i,:]
        a3i=a3[i,:]
        yi=y[i,:]


        delta3=(a3i-yi)#
        z2i=np.insert(z2i,0,np.ones(1))
        delta2=np.multiply(np.dot(delta3,theta2),dsigmoid(z2i))

        delta3=np.matrix(delta3)
        delta2=np.matrix(delta2)
        # print('delta3:',delta3.shape) #(1,10)
        # print('delta2:',delta2.shape) #(1,26)
        grad_theta2+=delta3.T.dot(np.matrix(a2i))
        grad_theta1+=delta2[:,1:].T.dot(np.matrix(a1i))
    grad_theta1/=m
    grad_theta2/=m

    lambda_theta1=theta1[:,1:]*lamda/m#计算正则项
    lambda_theta2=theta2[:,1:]*lamda/m

    grad_theta1[:,1:]+=lambda_theta1
    grad_theta2[:,1:]+=lambda_theta2

    grads={
        'grad_theta1':grad_theta1,
        'grad_theta2':grad_theta2
    }
    return grads
grads=backward_propagate(X,y_onehot,parameters)
grad_theta1=grads['grad_theta1']
grad_theta2=grads['grad_theta2']
print(grad_theta1.shape)
print(grad_theta2.shape)
grad_theta1[0,:10]
(25, 65)
(10, 26)

matrix([[2.75026728e-03, 4.78740411e-06, 8.57156752e-04, 1.43582353e-02,
         3.21817921e-02, 3.20213878e-02, 1.53658755e-02, 3.52853630e-03,
         3.28875302e-04, 1.67262973e-05]])
更新参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def updata_parameters(parameters,grads,learning_rate=1):
    theta1=parameters['theta1']
    theta2=parameters['theta2']#取出theta

    grad_theta1=grads['grad_theta1']#取出梯度
    grad_theta2=grads['grad_theta2']

    theta1=theta1-learning_rate*grad_theta1#梯度下降，更新参数
    theta2=theta2-learning_rate*grad_theta2

    parameters={
        'theta1':theta1,
        'theta2':theta2
    }
    return parameters
1
2
3
4
5
6
7
8
9
10
11
def progress(percent, width=50):
    '''
    进度打印功能
    :param percent: 进度
    :param width: 进度条长度
    '''
    if percent >= 100:
        percent = 100

    #show_str = ('[%%-%ds]' % width) % ((width * percent / 100) * "#")  # 字符串拼接的嵌套使用
    print('\r%s %f%%' % ('计算进度', percent), end='')
训练模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def nn_model(X,Y,parameters,epochs,learning_rate=1,lamda=1):
    J_list=[]
    for i in range(epochs):
        a3,cache=forward_propagation(X,parameters)#正向传播，计算个神经元的值

        grads=backward_propagate(X,Y,parameters,lamda=lamda)#反向传播，计算delta以求出参数theta1和theta2的梯度

        if i%50==0:
            J=cost_res(X,Y,parameters,lamda)#计算损失
            J_list.append(J)
            print('csot:',J)
        parameters=updata_parameters(parameters,grads,learning_rate)#进行梯度下降，更新参数
        recv_per = (100 * i/(epochs-1))  # 接收的比例
        progress(recv_per, width=30)  # 调用进度条函数，进度条的宽度默认设置为30
    return parameters
parameters=nn_model(x_train,y_train,parameters,1000,0.3) #lr=1 1000次 损失为0.73 正确率0.89
                                                     #1000  0.39 0.96
                                                    #l000 0.34  0.97
                                                    # lr=0.3 1000  损失：0.28  正确率0.98
csot: 0.3435146285670303
计算进度 4.904905%csot: 0.3332751302454119
计算进度 9.909910%csot: 0.33075159173284324
计算进度 14.914915%csot: 0.32867755006376664
计算进度 19.919920%csot: 0.3267981370452875
计算进度 24.924925%csot: 0.32501450922250563
计算进度 29.929930%csot: 0.32316574164765904
计算进度 34.934935%csot: 0.3182895333581057
计算进度 39.939940%csot: 0.31063714327553094
计算进度 44.944945%csot: 0.30796701871174065
计算进度 49.949950%csot: 0.30041283365746996
计算进度 54.954955%csot: 0.29823956515674244
计算进度 59.959960%csot: 0.2965327545282571
计算进度 64.964965%csot: 0.2949714724876018
计算进度 69.969970%csot: 0.29349755594339266
计算进度 74.974975%csot: 0.2920867477290434
计算进度 79.979980%csot: 0.2907250177923556
计算进度 84.984985%csot: 0.2894035835211862
计算进度 89.989990%csot: 0.2881215629635514
计算进度 94.994995%csot: 0.2868833407001544
计算进度 100.000000%
评估模型
1
2
3
4
5
6
7
8
9
10
11
from sklearn.metrics import classification_report
def show_accuracy(parameters, X, y):
    a3,cache=forward_propagation(X,parameters)
                                #选择结果最大的位置对应得数即为预测值
    y_pred = np.argmax(a3, axis=1) + 1#选择结果最大的那个数的索引值，给其加1即为预测的数
    y_true=np.argmax(y_test,axis=1)+1

    print(classification_report(y_true, y_pred))#打印正确率
    print(y_pred.shape)
show_accuracy(parameters,x_test,y_test)

              precision    recall  f1-score   support

           1       1.00      1.00      1.00        43
           2       1.00      0.98      0.99        42
           3       0.98      0.98      0.98        53
           4       0.94      0.94      0.94        34
           5       1.00      1.00      1.00        44
           6       0.96      0.94      0.95        48
           7       0.98      1.00      0.99        56
           8       0.98      0.98      0.98        42
           9       0.97      0.95      0.96        39
          10       0.94      0.98      0.96        49

    accuracy                           0.98       450
   macro avg       0.98      0.97      0.97       450
weighted avg       0.98      0.98      0.98       450

(450, 1)

1