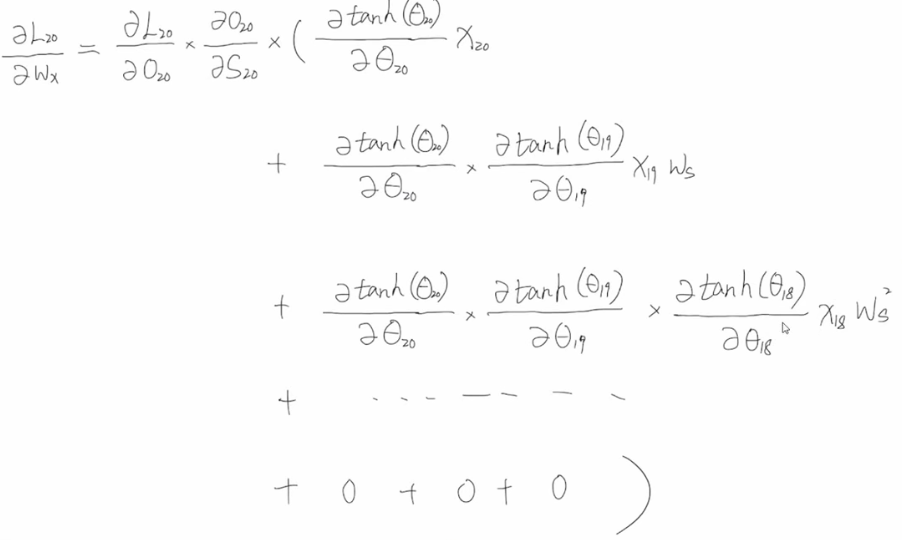传统神经网络弊端
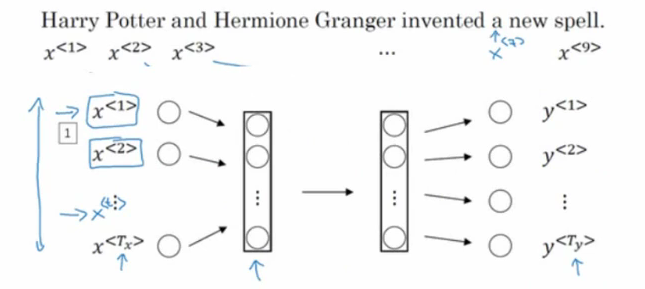
如上图所示,如果我们的输入是这样一句话,希望输出是其中的人名,如果我们使用标准的神经网络建模,就会出现如下问题:
①输入和输出数据在不同的例子中可能有不同长度。(每句话的长度都肯是不同的)
②一个像这样的神经网络结构,它并不共享从文本的不同位置上学的的特征。以前的特征输入是稳定的,即所有的特征表达的内容是同一性质的,比如人名是一个特征域类别,其他的是其他类别,一旦他们交换位置,是需要重新取学习的(即人名在一句话中出现的位置是不固定的),如果神经网络已经学习到了在位置1出现的Harry是人名,那么如果Harry出现在其他位置,可能就识别不出来了。
③参数量巨大。输入网络的特征往往是one hot或embedding向量,维度较大,并且输入网络的特征是一段序列,当这段序列很长的时候,输入量是巨大的。
④没有办法体现时序上的前因后果(比如翻译)。
RNN循环神经网络
网络结构
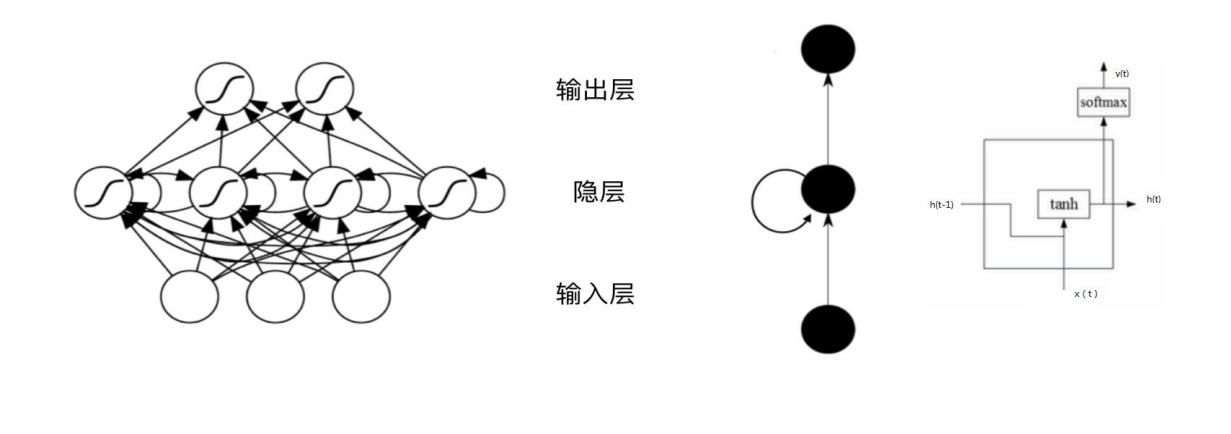
一个典型的循环神经网络结构如上图所示.我们可以发现RNN的隐藏层与传统神经网络之间有所不同。我们将其隐藏层展开,RNN将每个时间状态关联了起来,当前状态不仅受当前输入的影响,也受上一时刻的状态的影响。
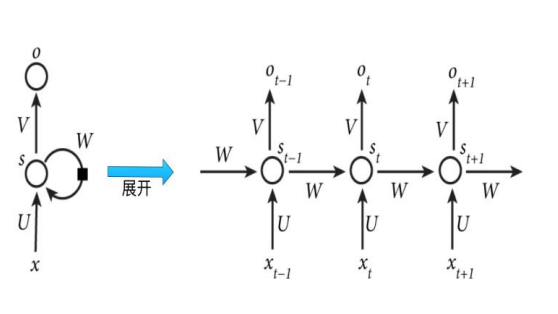
下面我们来看一下RNN是怎样运算的。下图是其中一个隐藏层单元。其中at是当前状态,xt是当前输入。
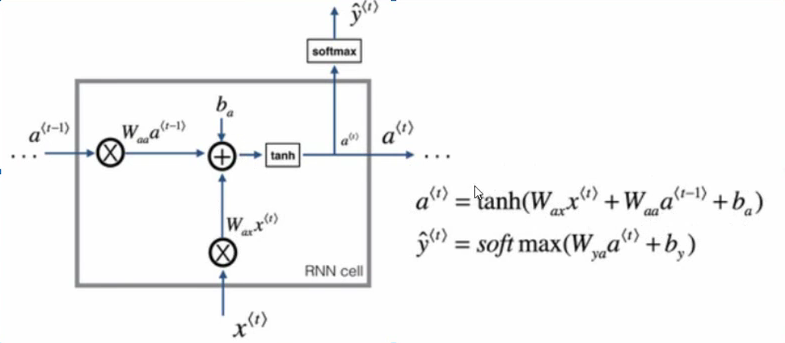
当前状态为a(t)=tanh(waxx(t)+waaa(t−1)+ba)
当前输出为 y(t)=softmax(wyaa(t)+by)
,这里的激活函数可根据任务目标进行替换。
这里也很好理解,可以用人脑来比喻,加入一对情侣在上一时刻吵架了,在这一时刻女方闺蜜又来火上浇油,这时女方可能会在闺蜜的影响下更加生气,即当前状态还受到上一状态影响。
RNN循环神经网络的特点为:隐藏层为串联结构,体现出“前因后果”,后面结果的生成要参考前面的信息。并且与卷积神经网络一样,所有特征共享一套参数,面对不同的输入,能够学到不同的相应结果,由于参数共享极大减少了训练参数量,输入和输出数据在不同例子中可以右不同的特征。
前向传播
在前面的单个隐藏层神经元计算中已经说了,这里不在啰嗦了。

损失函数
由于RNN在每个时刻都有输入和输出,其单个时间步的损失函数可以自定义,对于二分类任务我们可以使用交叉熵作为我们的损失函数,Lt(yt^,yt)=−ytlog(yt)−(1−yt)log(1−yt^)
.整个时间序列的损失函数就是将每个时间步的损失加起来L(yt^,yt)=∑t=1TLt(yt^,yt)
反向传播
有了损失函数,我们就可以运用反向传播来最小化代价函数。
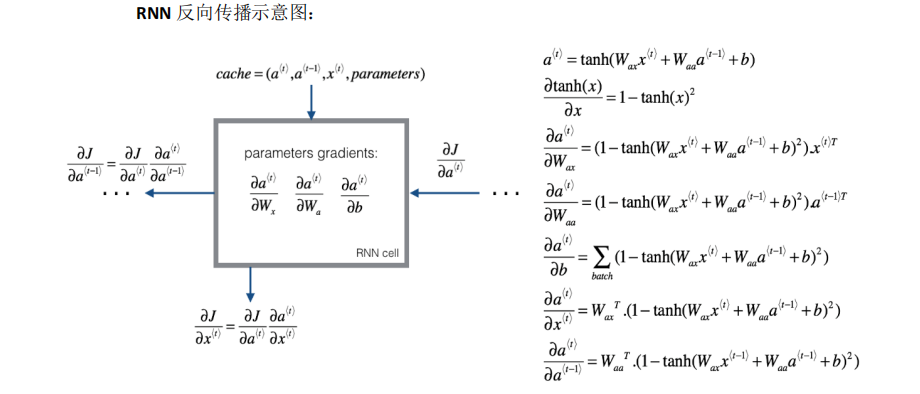
RNN的缺点
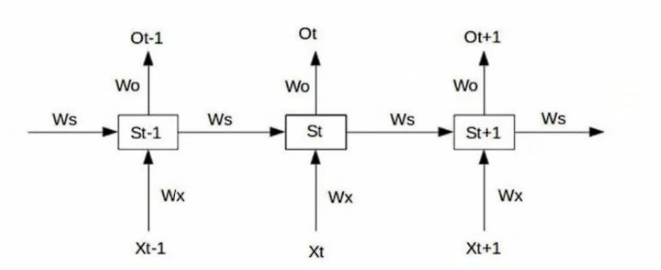
假设我们的RNN模型如图所示。则我们可以计算出
s1=tanh(wxx1+wss0+b1) o1=wos1+b2
s2=tanh(wxx2+wss1+b1) o2=wos2+b2
s3=tanh(wxx3+wss3+b1) o3=w0s3+b2
我们使用平方差作为损失函数,则在t=3时刻,损失函数为L3=21(Y3−O3)2,在进行反向传播要求的梯度参数wo,wx,ws,b
∂wo∂L3=∂o3∂L3∂wo∂o3=(o3−y3)∂wo∂o3
∂wx∂L3=∂o3∂L3∂wx∂o3=∂o3∂L3∂s3∂o3∂wx∂s3
令θ3=wxx3+w2s2+b1
wxs3=∂θ3∂tanh(θ3)∂wx∂θ3=∂θ3∂tanh(θ3)(∂wx∂wxx3+∂wx∂wss2)=∂θ3∂tanh(θ3)x3+∂θ3∂tanh(θ3)∂wx∂s2ws
同理可得:
∂wx∂s2=∂θ2∂tanh(θ2)x2+∂θ2∂tanh(θ2)∂wx∂s1ws
∂wx∂s1=∂θ1∂tanh(θ1)x1
所以:
wxs3=∂θ3∂tanh(θ3)x3+∂θ3∂tanh(θ3)∂θ2∂tanh(θ2)x2ws+θ3∂tanh(θ3)∂θ2∂tanh(θ2)∂θ1∂tanh(θ1)x1ws2
再次代入得
∂wx∂L3=∂o3∂L3∂s3∂o3∂wx∂s3=∂o3∂L3∂s3∂o3(∂θ3∂tanh(θ3)x3+∂θ3∂tanh(θ3)∂θ2∂tanh(θ2)x2ws+∂θ3∂tanh(θ3)∂θ2∂tanh(θ2)∂θ1∂tanh(θ1)x1ws2)
整理得:
∂wx∂L3=k=1∑3∂o3∂L3∂s3∂o3(j=4−k∏3∂θj∂tanh(θj))x4−kwsk−1
则任意时刻得损失为
∂wx∂Lt=k=1∑t∂ot∂Lt∂st∂ot(j=t+1−k∏t∂θj∂tanh(θj))xt+1−kwsk−1
ws与wx得求法一样这里不在求了。
我们可以看到ws是k-1次方项,当ws很小时,其在经过次方计算后就会逐渐变为0,从而导致梯度消失。
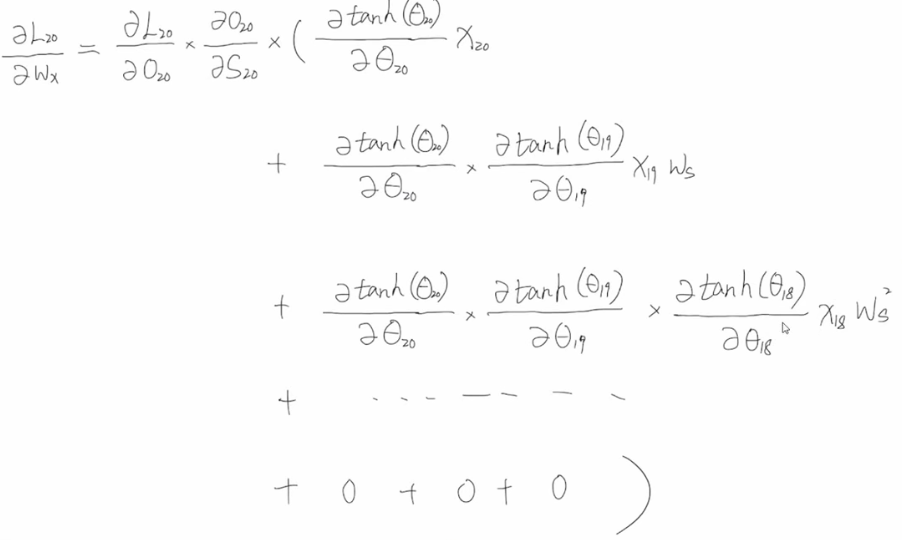
当t=20时的时,当ws比较小时,在次方较高时就会变成了0,那么之前时刻对当前状态的影响就传不到这里来了。
这里举个例子:有一句话为The cat,which ate already,…,wsa full.这里后面用was还是were是由前面的cat的单复数形式决定的,一旦中间的这个which句子很长,cat的信息根本传不到was这里来,对was的更新学习就起不到任何作用。
而当ws即使稍微大于1时最终就会非常大,从而造成梯度爆炸,解决办法就是梯度修剪,即观察梯度向量,如果它大于某个阈值,就缩放梯度向量,保证它不会太大。
(补充:)
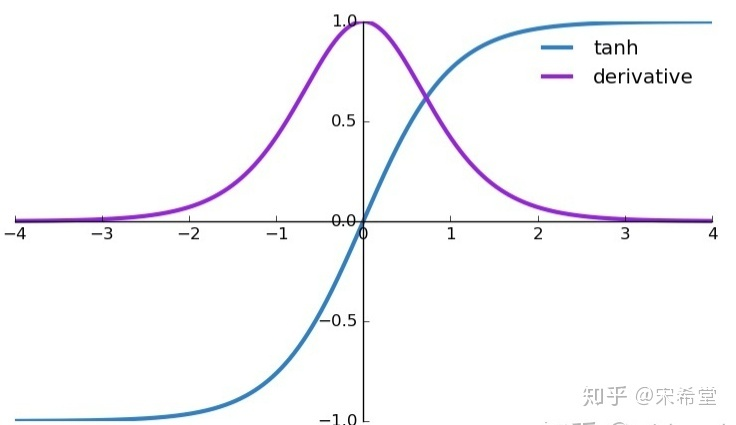
这是tanh激活函数的函数图和导数图:我们可以从图中可以看出,tanh函数导数值[0,1]的,我们的式子中有∂θj∂tanh(θj)的连乘项,如果连乘的项数过多,则也又可能会导致梯度消失,但与ws的次方项相比并不是主要原因。
LSTM(长短期记忆神经网络)
由于在输入序列较长时RNN容易造成梯度消失,所以提出了LSTM得概念,其思路是设计一个记忆细胞,具备选择记忆得功能,可以选择记忆重要信息,过滤掉噪声信息,减轻记忆负担。
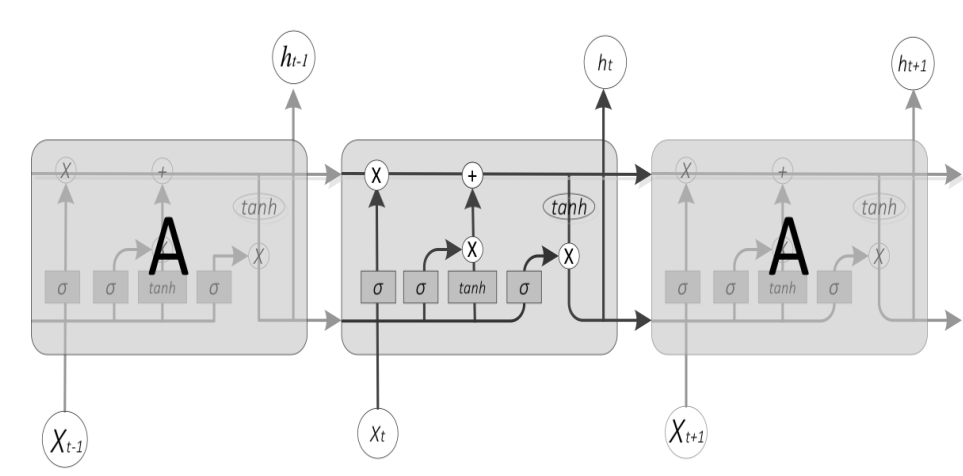
我们可以看到LSTM比RNN要复杂了许多,其主要区别就是增加了记忆细胞。下面我们来详细介绍这个记忆细胞是怎样工作的。
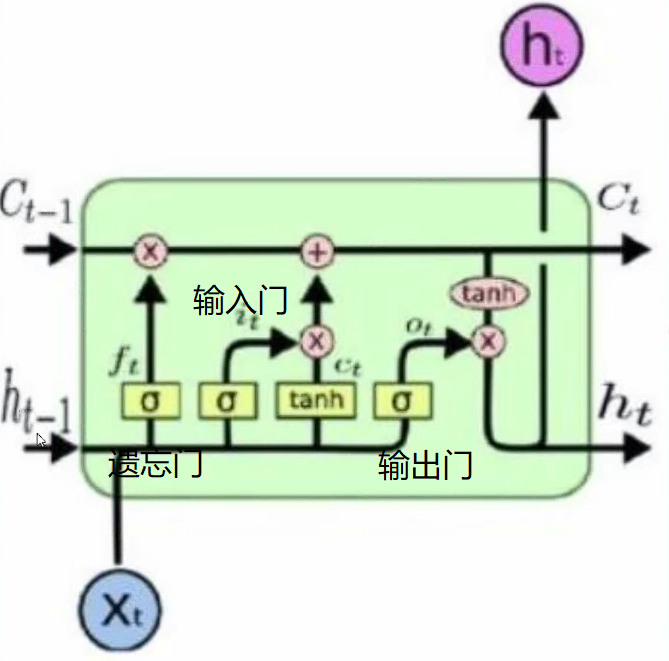
我们以一个单元来做介绍,其中Ct代表当前时刻得记忆状态,ht表示当前时刻得状态。一个单元主要由三个门组成:遗忘门,输入门,输出门。
前向传播过程
ft=σ(wxfxt+whfht−1+bf) σ为激活函数
ct’=tanh(wxcxt+whcht−1+bc)
it=σ(wxixt+whiht−1+bi)
ct=ct−1⋅∗ft+ct’⋅∗it
ot=σ(wxoxt+wh0ht−1+bo)
mt=tanh(ct)
ht=ot⋅∗mt
yt=wyhht+byh(输出是具体情况而定,可以加激活函数)
在LSTM的每个时间步里面,都有一个记忆细胞cell(ct部分),这个东西给予了LSTM选择记忆功能,使得LSTM有能力自由选择每个时间步里面记忆的内容。
长短期记忆网络的步骤为:
-
决定从元细胞状态中扔掉那些信息。由叫做“遗忘门”的sigmoid层控制,遗忘门会输出0~1之间的数,1表示保留该信息,0表示丢弃该信息。
-
通过输入门将所有有用的新信息加入到元细胞状态。首先,将前一状态和当前状态的输入输入到sigmoid函数中率除掉不重要信息。另外,通过tanh函数得到一个-1~1之间的输出结果。这将产生一个新的候选值,后续将判断是否将其加入到元细胞中。
-
将上一步中sigmoid函数和tanh函数的输出结果相乘,并加上第一步中的输出结果,从而实现保留的信息都是重要信息,此时更新状态即可忘掉那些不重要的信息
-
最后,从当前状态中选择重要的信息作为元细胞状态的输出。首先,将前一隐状态和当前输入值通过sigmoid函数得到一个0~1之间的结果值,然后对第三步中输出结果计算tanh函数的输出值,并与得到的结果值相乘,作为当前元细胞隐状态的输出结果,同时也作为下一个隐状态的输入值。
我们带入期末考试这样一个场景,假设我们上一时刻考的是高等数学,这一时刻我们要考线性代数。xt相当于复习,ct表示复习中产生的记忆,ht表示考完线性代数后的状态,则ht−1是考完高等数学后的状态,ct−1表示复习高等数学时产生的相关记忆。
在复习线性代数时,我们想尽可能的忘掉与线性代数无关的东西,通过遗忘门,我们可以以往掉泰勒公式,傅里叶级数等与考线性代数没有什么帮助的知识给遗忘掉,而把基本运行,求导,求微分这样有帮助的知识给保留下来。
输入门中的ct’表示再复习中生成的新的记忆,但这些记忆也并不是全都有用,比如我们在复习的过程中看了一些相关的数学家的奇闻轶事形成了相关的记忆,但是这部分记忆对我们的考试没有什么作用,所以我们要通过输入门将这些无用的信息给过滤掉,只记住与考试相关的记忆。ct是我们的当下记忆,显然应该是当前复习学得的记忆与记过遗忘门后保留的对我们考试有关的记忆相加和。
输出门要做的就是将复习的到的记忆给转换成答题的过程,我们在思考一道题时需要我们运用复习来的知识进行答题,而我们复习到的东西也并不一定全部都会考到,所以要通过ot将考试需要用到的知识提取出来。
反向传播
推导过程较复杂,这里不写了。下面的截图均来自视频。
具体视频推导
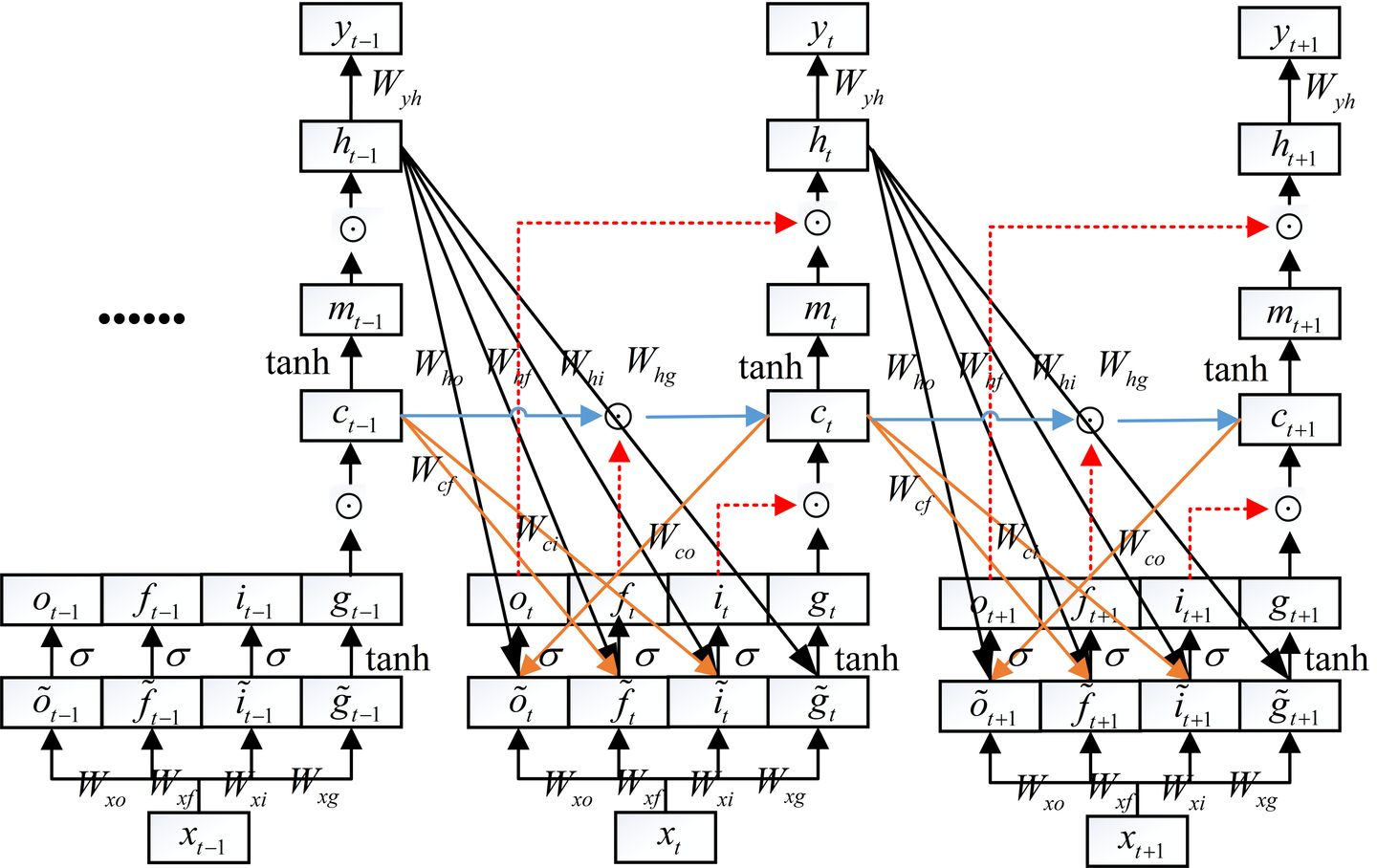

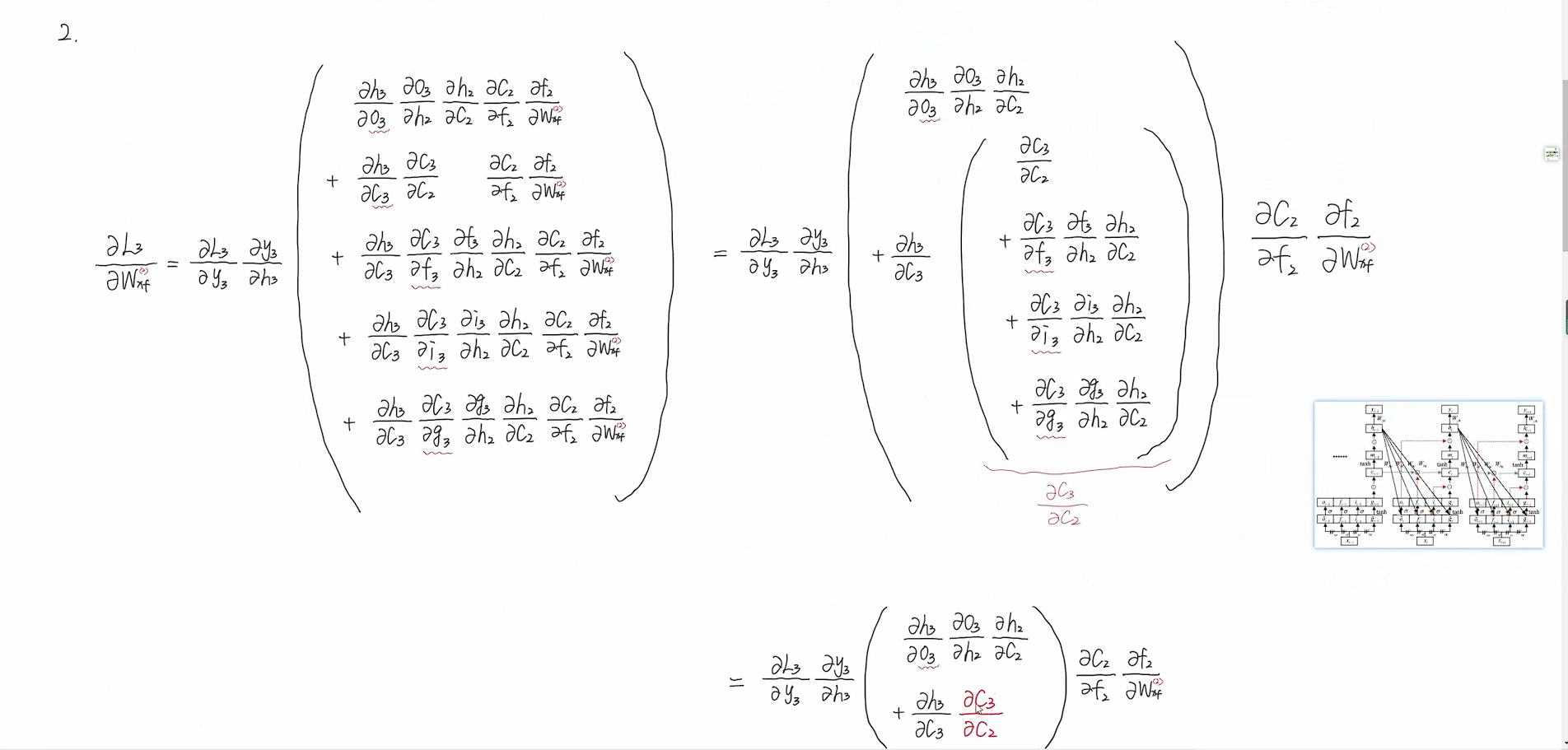
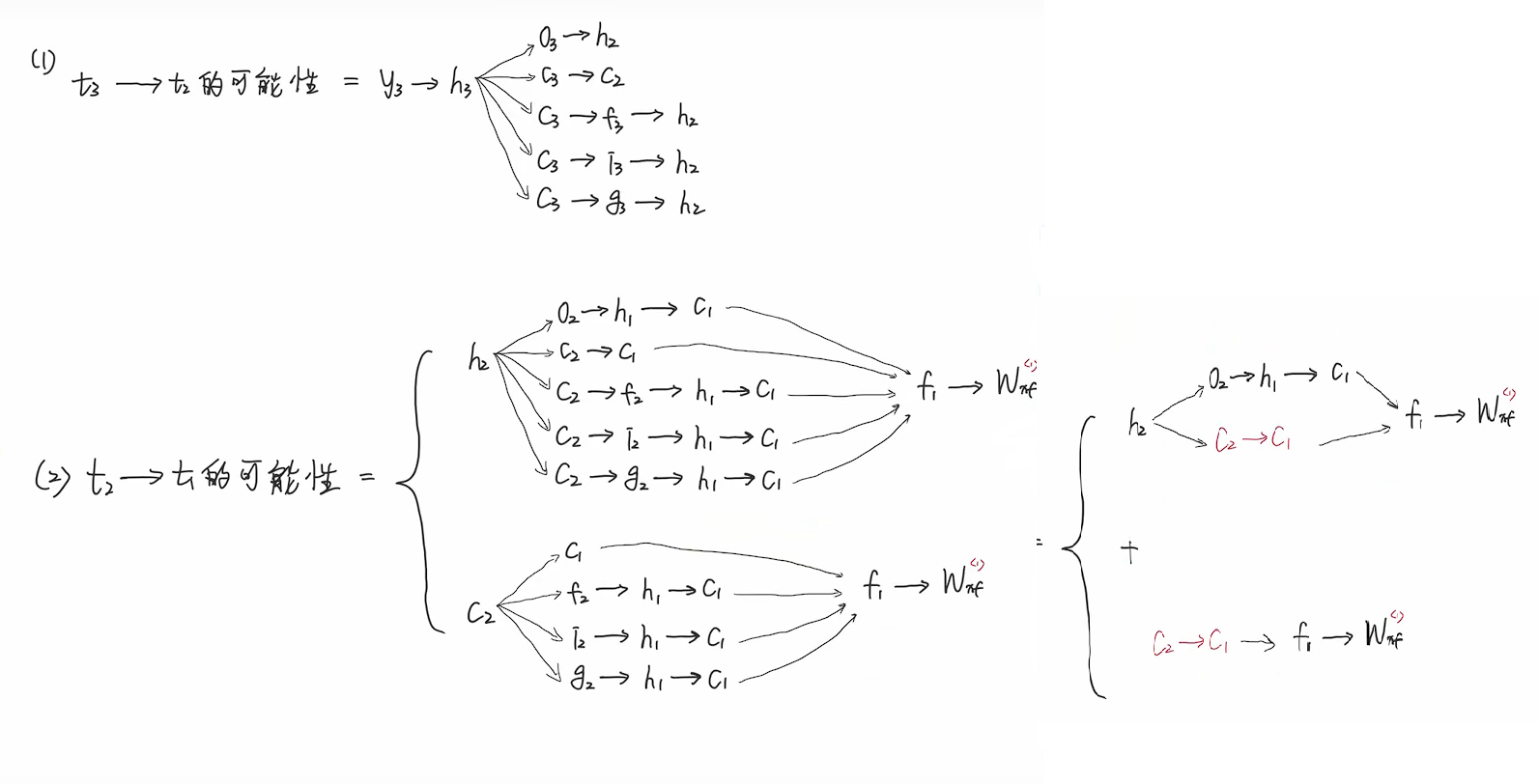
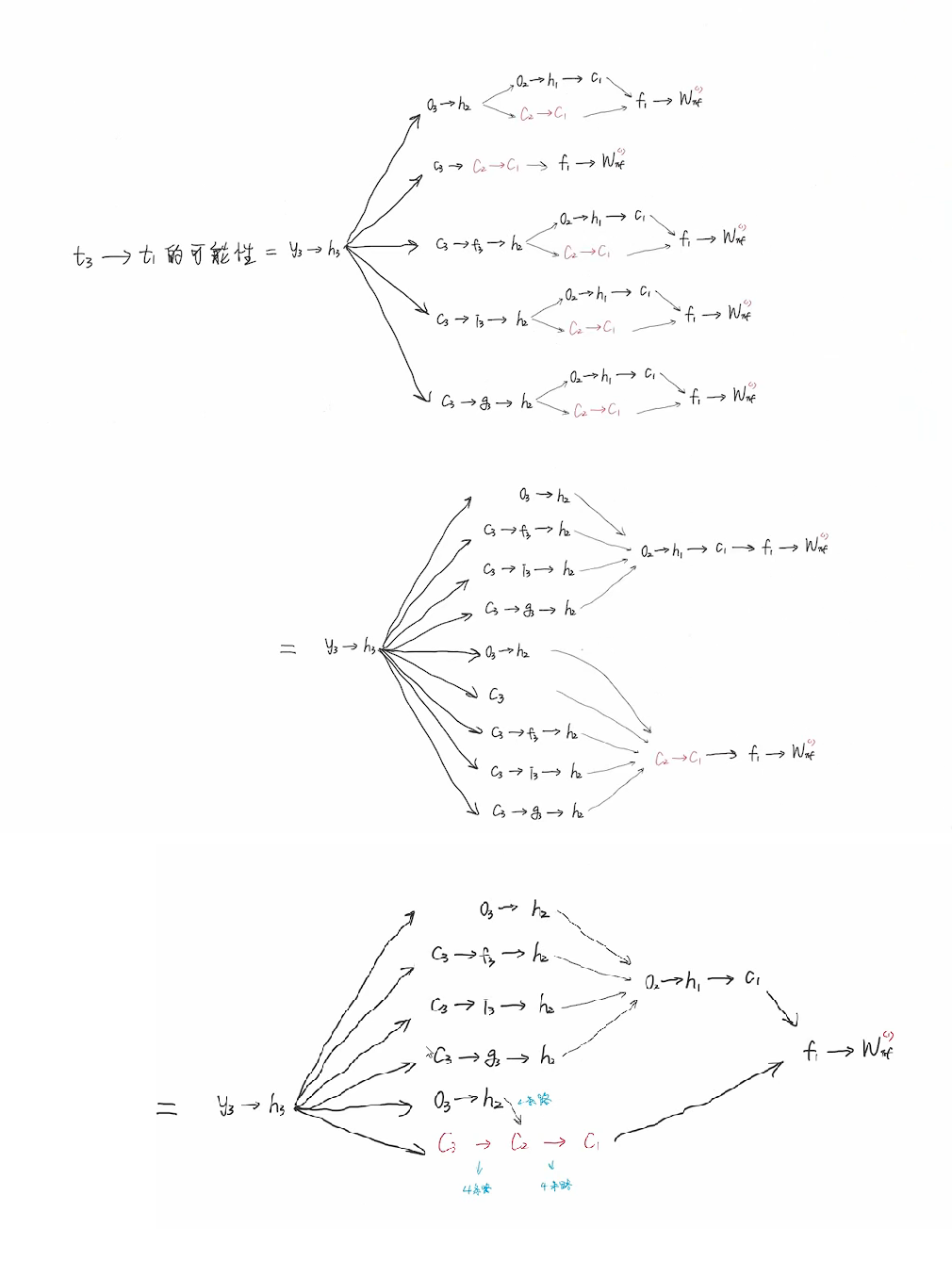
c3到c2有4条路径,c2到c1也有4条路径,所以y3到wxf共有16+4+4=24条路径。
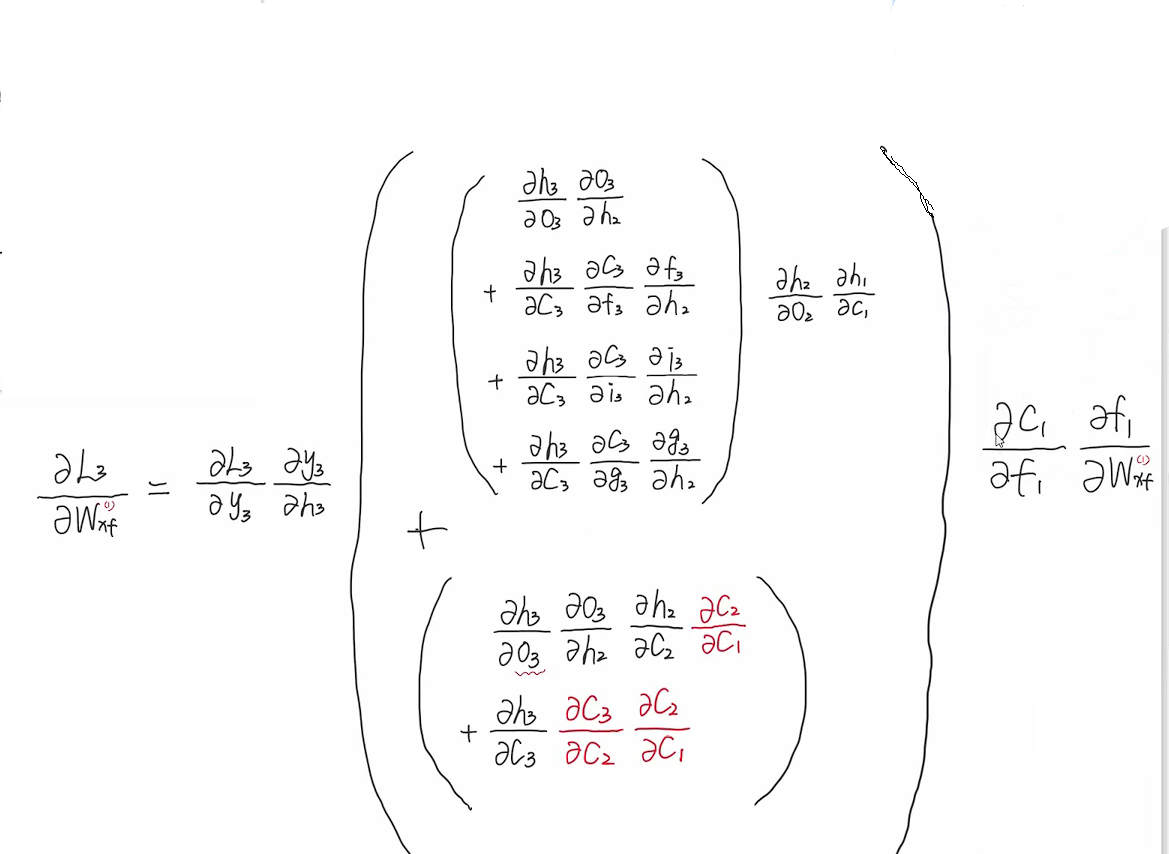

模型可以通过学习,通过多个参数的学习以达到ct−1ct来达到接近于1,从而令多项连乘近似等于1∗1∗1...∗1的效果。

GRU网络
网络结构
GRU是LSTM网络的一种简化形式,在LSTM中引入了三个门函数:输入门、遗忘门和输出门来控制输入值、记忆值和输出值。而在GRU模型中只有两个门:分别是更新门和重置门,具体结构如图所示:
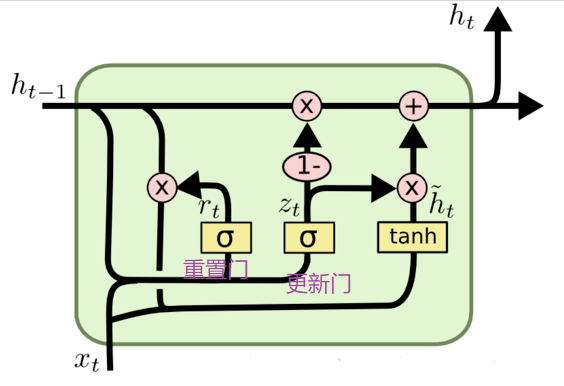
更新门用于控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门控制前一状态有多少信息被写入到当前的候选集 h~t 上,重置门越小,前一状态的信息被写入的越少。
前向传播
GRU的前向传播公式如下:
rt=σ(Wr⋅[ht−1,xt])
zt=σ(Wz⋅[ht−1,xt])
ht^=tanh(Wh^⋅[rt∗ht−1,xt])
ht=(1−zt)∗ht−1+zt∗ht^
yt=σ(Wo⋅ht)
其中[]表示将两个向量拼接,*表示矩阵的乘积。
首先,我们先通过上一个状态和当前输入xt来获取两个门控信号.
我们仍然举例来理解:

ht−1表示先前我们再学习过程中整理的笔记,xt表示我们当前想要学习机器学习,而rt则相当于与机器学习有关的笔记的相关系数。我们可以通过rtht−1来提取出与机器学习相关的部分笔记。再与xt进行拼接再经过tanh函数学习出了一份新的笔记,再我们的新笔记中仍然包含着与机器学习无关的内容,所以我们项去剔除与机器学习无关的笔记。

我们的zt(更新门来保留与机器学习相关的笔记)。(1−zt)∗ht−1来保留我们原来的笔记中与机器学习有关的内容,zt∗ht^来保留我们整理出的新的笔记中与机器学习有关的内容,再将二者加起来。

与LSTM区别
与LSTM相比,GRU的参数更少,因此其训练速度更快,或着说需要归纳的数据更少。但相应的,如果有足够多的训练数据,LSTM的表达能力或许更强。相较于LSTM,由于参数的减少,GRU能降低过拟合的风险。