卷积神经网络
卷积
对于连续型函数f,g,f函数和g函数的卷积公式为:
f和g函数做卷积的实质是先对g函数取反然后在平移一个n在于f函数相乘在相加。

对于离散函数,f函数和g函数的卷积公式为:
(n相当于步长)
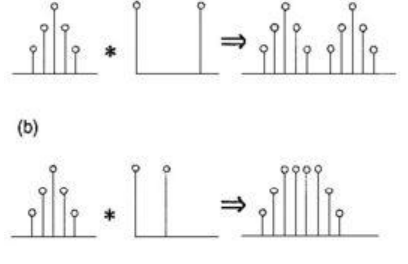
我们从图中可以看出,无论是连续型或者是离散型函数,做完卷积以后,得到的新的函数仍然保留了原来的函数的特征(比如对于连续型函数其卷积以后的图像趋势与原来的函数趋势仍非常相似),所以卷积可以认为是一个滤波器,g函数对f函数做卷积,可以把f函数的重要特征抓取,非重要特征舍弃。
图像的编码与卷积
对于一个图采用像素编码。以32像素的灰度图为例,将一个图片的横向和纵向分别用32个像素进行编码,每个像素取值是0到255。像素越少处理的速度越快,当然特征损失的也会更多。

那么该如何获得图的特征的,我们很容易就想到了卷积。对图进行编码以后就相当于得到了一个f函数,要想通过卷积获得图的特征我们就需要找一个g函数,我们将这个g函数命名为和函数。
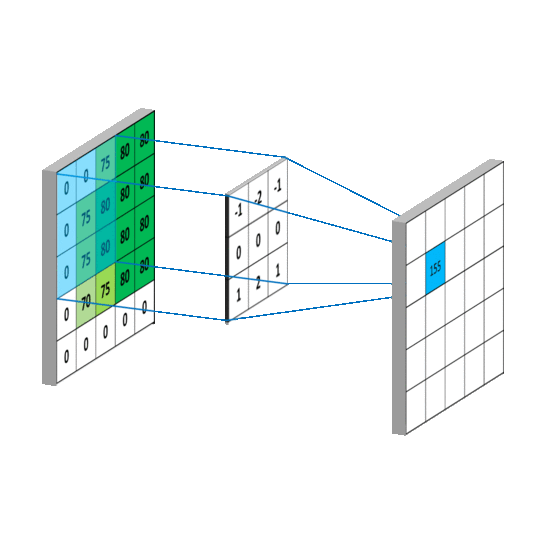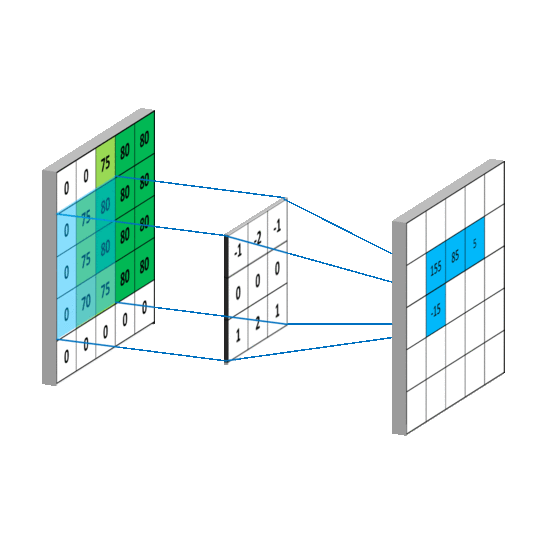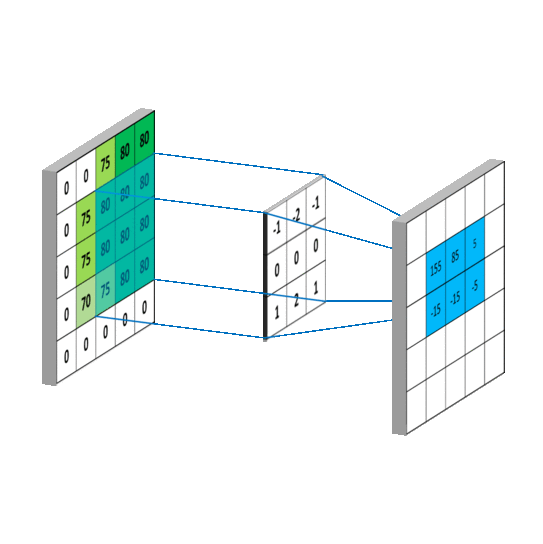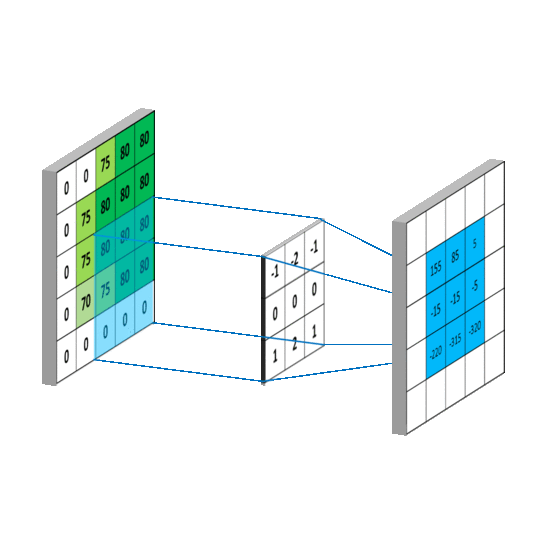
我们发现在做完卷积后,图的编码矩阵小了一些,说明通过卷积后我们的特征变少了,但重要特征保留了下来。

我们从图中可以看到,卷积的计算过程就是相同位置想成相加,通过卷积操作将4个像素压缩为了1个像素,做卷积的实质就是过滤掉图的不必要特征,保留其重要特征。,接着移动一个步长,在与卷积核对于位置相乘相加做卷积。
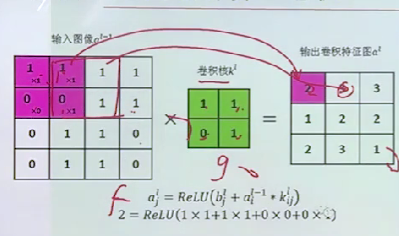
在对整个图做完卷积后,我们得到了一个较小的特征图。由于在做卷积时在图的边缘部分只做了一次操作,处有时候我们为了获得边缘特征,我们采用Padding的方式来获得边缘处特征.(Padding即在图的特征矩阵外围补0)
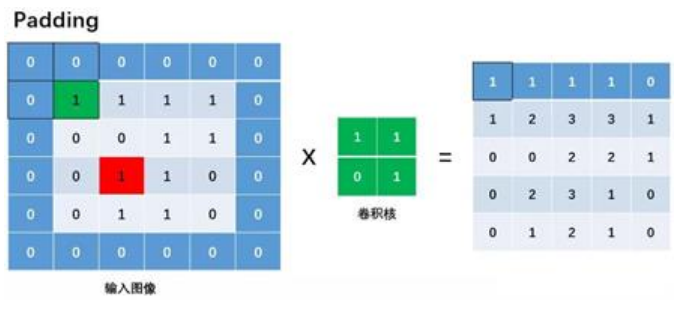
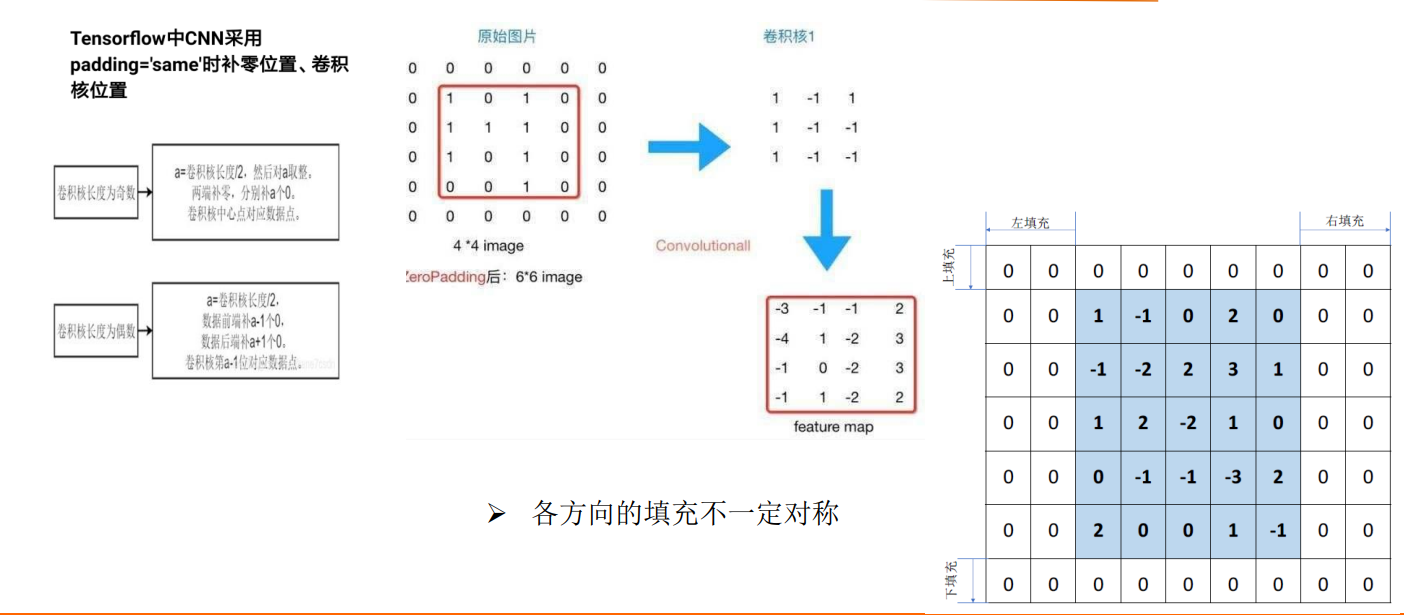
对于如下一张图,我们对其进行编码以后用一个3*3的卷积核做卷积得到特征矩阵,将特征图还原为图像以后(右图所示),我们可以看到,特征图与原来的图相比虽然变模糊了,但是有关原始图像的重要特征,人,衣服等的轮廓都显示了出来。
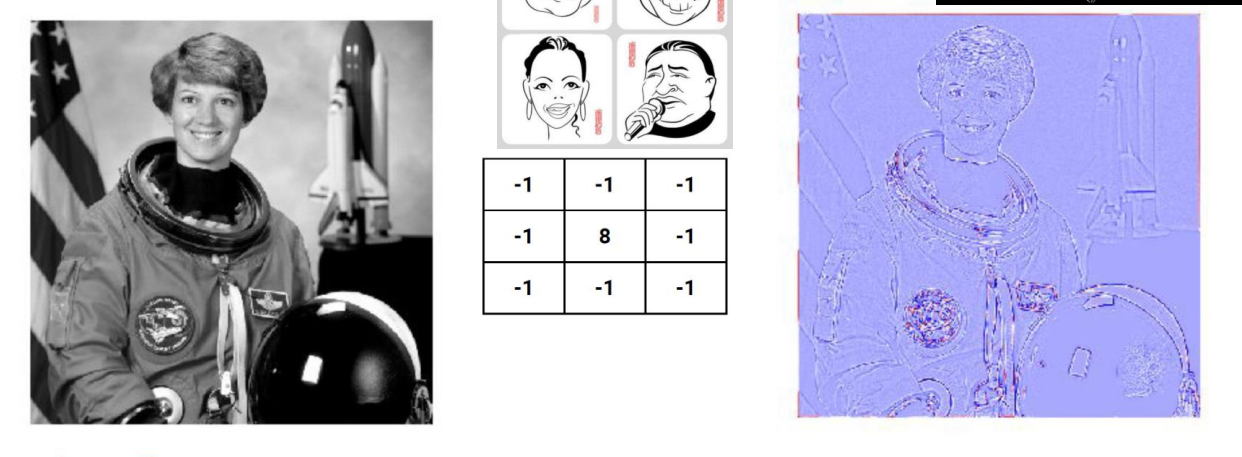
原始图做完卷积后的特征图大小为:
其中为特征图的大小,为输入的原始图的大小,p为padding操作加的0的层数,f为卷积后的大小,S为步长,即每次做完卷积后移动的大小。
如一个输入为的矩阵,卷积核为大小的,我们的步长为1,不做padding操作,所以我们应得到一个,及最后得到一个的特征矩阵,如果步长为2应得到(7-3)/2+1=3的特征矩阵。
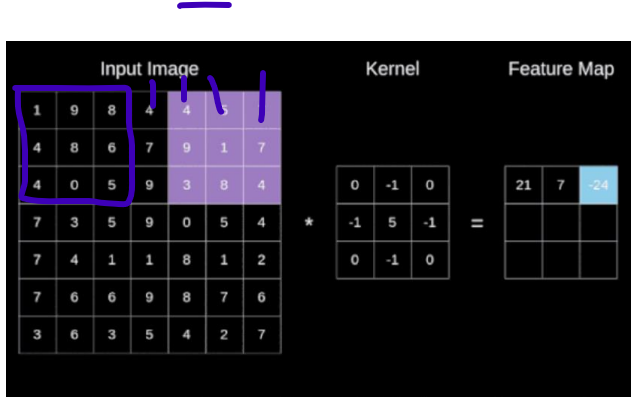
对于这个式子我们很容易理解,输入是的矩阵,卷积核是的,如图所示在左上角做完卷积后,如果步长为1,则应该只剩下列可以移动了(图中紫线所示),再加上未开始移动时做的一次卷积最终得到的特征大小就是5。
我们这里的都是横向和纵向像素大小对称的,如果不是对称的,我们就需要对横向和纵向方向分别进行计算。
多通道卷积
对于同一张图我们可以用不同的卷积核获得不同的特征图。如果我们想要获得x方向的特征,我们的卷积核可以水平方向1多一点,y方向的0多一些。获得y轴方向的卷积核可以x轴方向0多一点,y方向1多一点。

由于一个图有很多的特征,而一个卷积核只能获得某一个方向的特征,所以我们为了获得更多方向的特征就会采用多个卷积核,获得不同方向的特征后进行叠加。
对于彩色图,一个图的任意一个像素的任意颜色,我们都可以将其分为RGB三个不同颜色的值。所以对于一个彩色图,我们可以用三个矩阵(红,蓝,绿)来编码表示。
对于彩色图,我们就可以采用多通道卷积对其进行卷积。即红蓝绿三个不同的通道分别对同一个卷积核做卷积,最后将得到的三个通道的特征矩阵进行合成(相应位置相加即可).
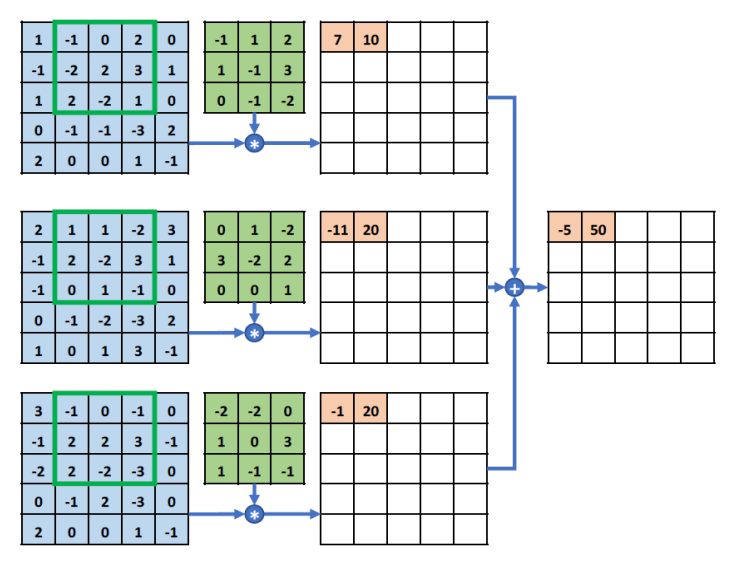
池化
又是我们为了进一步压缩数据,还会在做完卷积以后进行池化操作,以此达到降维,去除冗余信息,简化网络复杂的的目的。
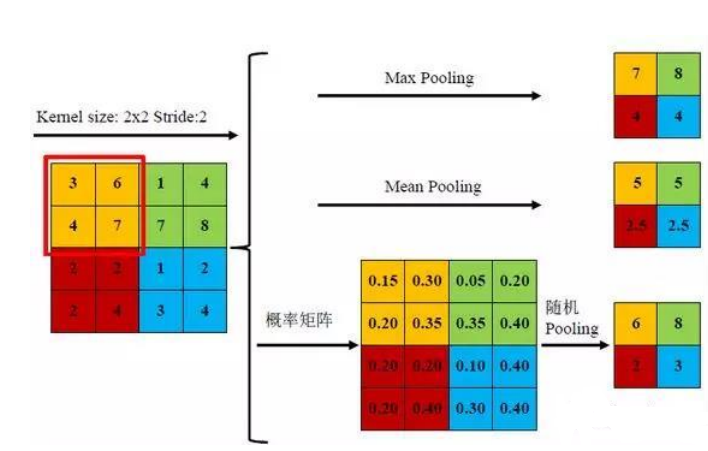
池化主要有两种:平均池化和最大池化。对于平均池化,
加入我们的原始矩阵为上图大小的矩阵,池化核大小为的矩阵,步长为2,进行平均池化操作就是对原始矩阵的每一个像素矩阵求平均值,对于上图的红色线条圈住的像素矩阵对其进行平均池化得到的结构就是。最终得到了一个的矩阵,平均池化最主要作用就是对特征进行压缩,虽然损失了部分信息,但还是保留了一些重要特征,比如颜色特征求平均值后深得颜色还是深,浅的颜色还是浅。最大池化操作就是取像素矩阵中的最大值,上图红色线圈部分的最大池化就是。最大池化主要作用就是突出了每个区域的最主要特征。
LeNet模型
LeCun在1998年提出了LeNet,并成功应用于了美国手写数字识别,并且测试误差率小于1%,是最早的卷积神经网络模型。下图就是Lenet模型的结构图,下面我们逐层来进行介绍。
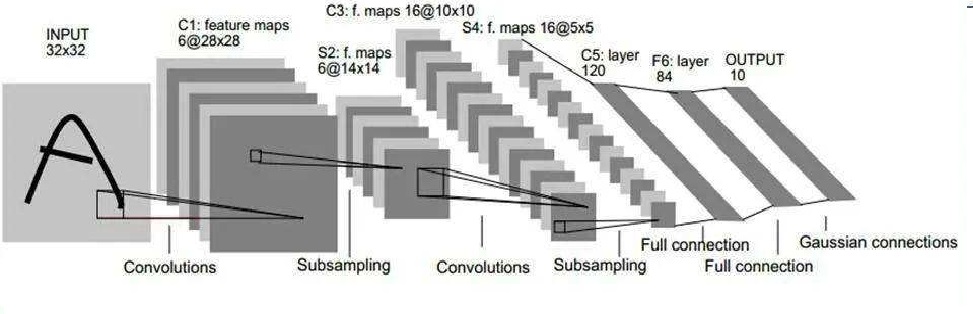
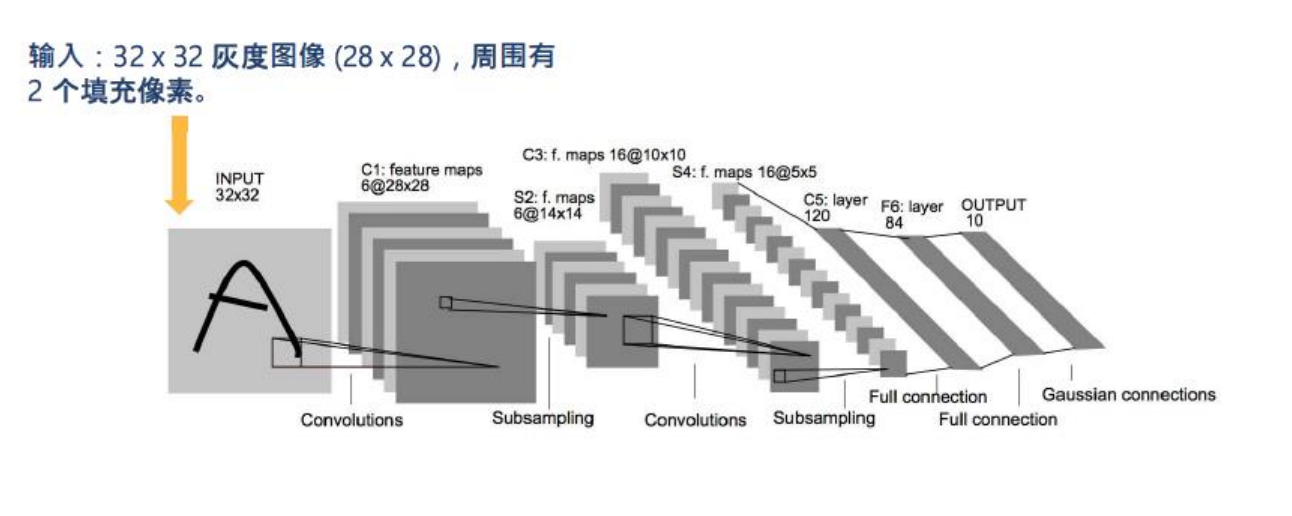
输入层我们采用像素的编码,在经过padding预处理后成为了的矩阵。
第一个卷积层
第一层我们采用6个卷积核在6个通道分别对图的编码进行卷积操作。这里的卷积核大小为的,则得到6个大小的特征矩阵。
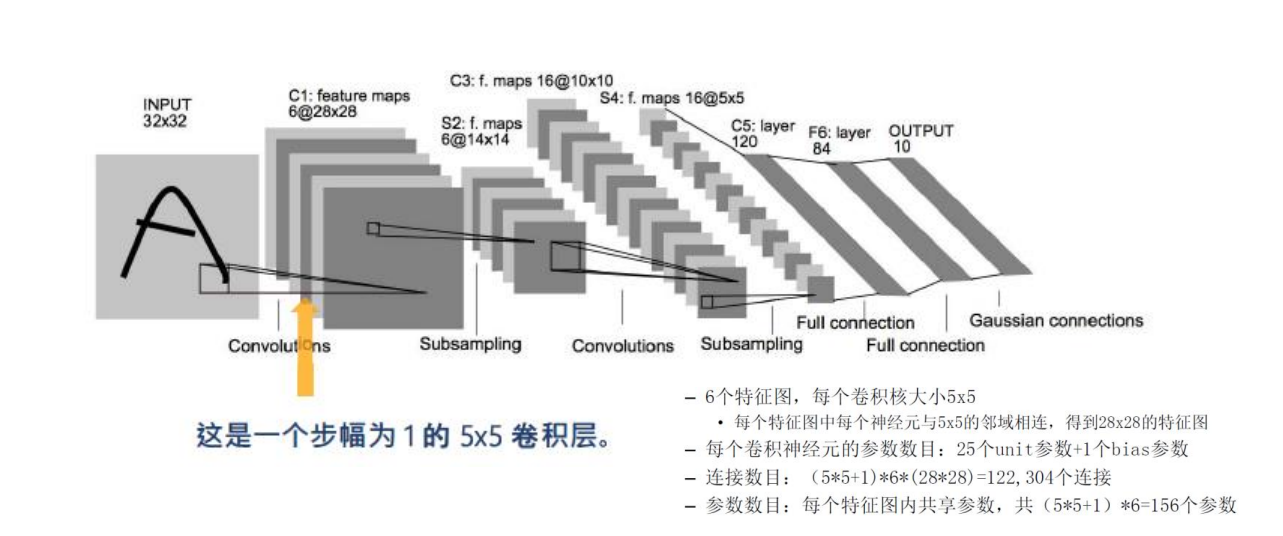
与全连接神经网络不同的是,卷积神经网络采用共享权重的方式进行连接,通过卷积运算我们可以知道,输入层的每一个的像素矩阵对应一个特征矩阵的一个像素,
由于卷积是对图片的不同部位做特征提取,所以一个通道内,其卷积核是相同的,每一个输出层的的像素矩阵与第二层相连接时的参数应该是相同的,所以从输入层到第一个卷积层的参数数目为,1是代表卷积层每个通道的神经元的偏置,乘6是应为参数只在每个通道内共享,在不同通道是不一样的。其连接数目为,这里可以理解为每一个通道每个像素都对应一个的输入层的像素矩阵。所以我们可以看出卷积神经网络中连接数目是远远小于参数数目的,所以我们在进行梯度下降法进行优化时要优化的数目就会大大降低。
第一个池化层
接着我们在卷积层后面添加了一个池化层。其池化核大小为的矩阵,步长为2,最终的输出的大小为,所以得到了的输出矩阵。
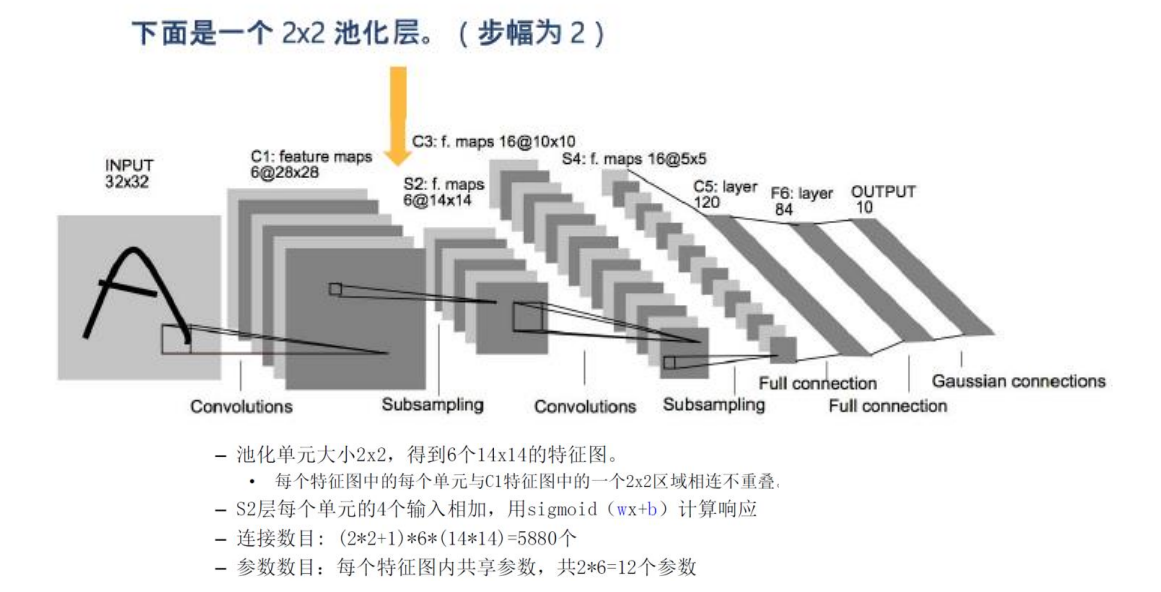
那么卷积层和池化层是怎样连接的呢?由于池化核是的,所以卷积层一个的像素矩阵对应池化层1个像素,所以一个区域的像素矩阵会与池化层的一个像素有4条连线,而与做卷积时不同,在这里4条连线我们只记1个参数,(只记一个是因为这里的计算方式是每个区域四个元素相加,用sigmoid(wx+b)来计算输出,所以只有一个参数),所以卷积层到池化层的参数数目为个,+1在这里仍然是池化层神经元的偏置,参数仍然是在相同通道内共享,不同通道间不共享。而连接数目为个。
第二层卷积层
仅仅只进行一层卷积和池化是不够的,所以我们右添加了一层卷积层和池化层。
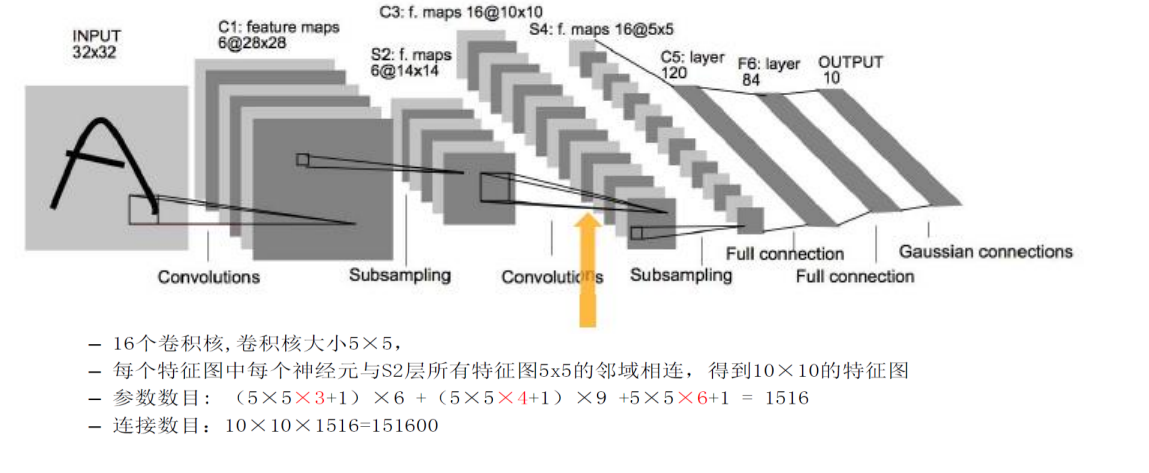
第二层池化为了能够更加精细化获取图片的特征,我们运用16个通道来进行卷积操作来获得更多特征。在该层的卷积核大小仍然为的,所以输出的大小为,即获得了大小的输出矩阵,而这个卷积层最终获得了16个通道的输出矩阵,那么问题来了6个通道是如何变成16个通道的呢?
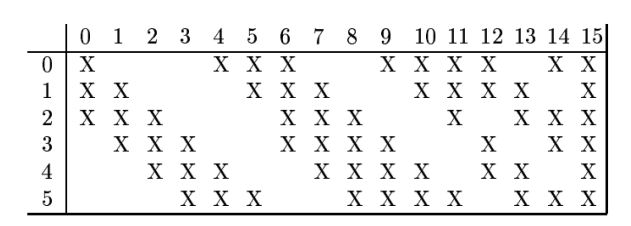
请看上图,图中竖直方向从0到5的编号分别代表上一层的6个通道的编号,0到15是代表16个通道的编号。我们采用16个卷积核对这6个通道做卷积,其对应方式边如图所示,比如本层第一个通道的卷积核要对上一层的第0,1,2三个通道的输入分别做卷积,再将得到的3个特征图进行叠加得到第一个通道的特征矩阵。
这两层之间的参数数目为,6,9,1分别对应上表中对上层3个通道,4个通道,6个通道分别做卷积的通道的数目。由于参数在不同通道间是不共享的,拿第一个通道来说,要对上一层3个通道分别做卷积,所以其参数应该是每一个通道的参数数目在乘以通道数,即,+1仍然是神经元的偏置。其连接数目为10101516=151600.
第二层池化层
这里仍然采用的池化核,最终得到了的输出矩阵。
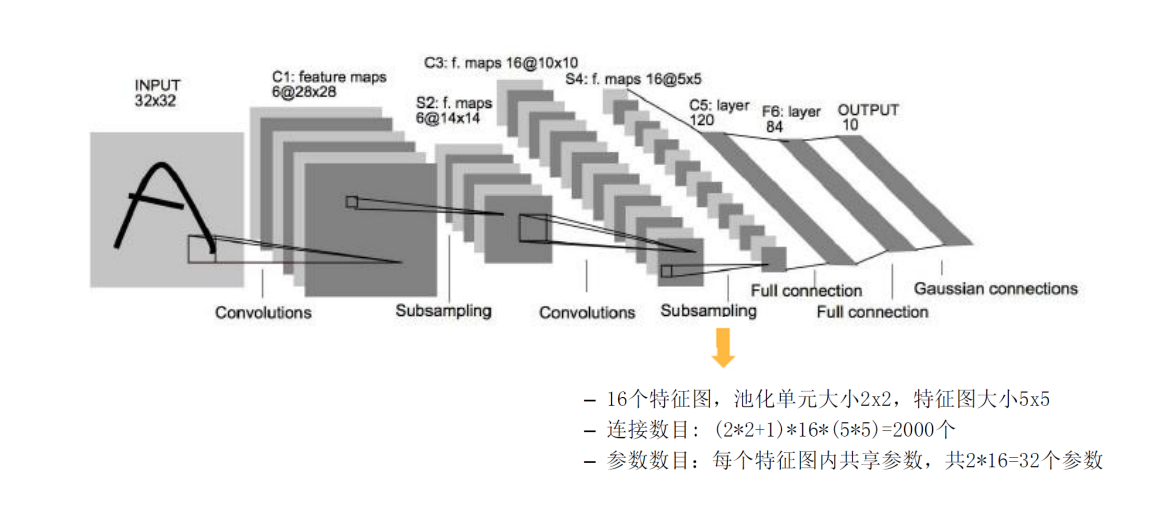
所以卷积层与池化层的参数数目为,其连接数目为个。其中+1仍然是神经元偏置,参数仍然是在相同通道内共享,不同通道内不共享。
全连接层
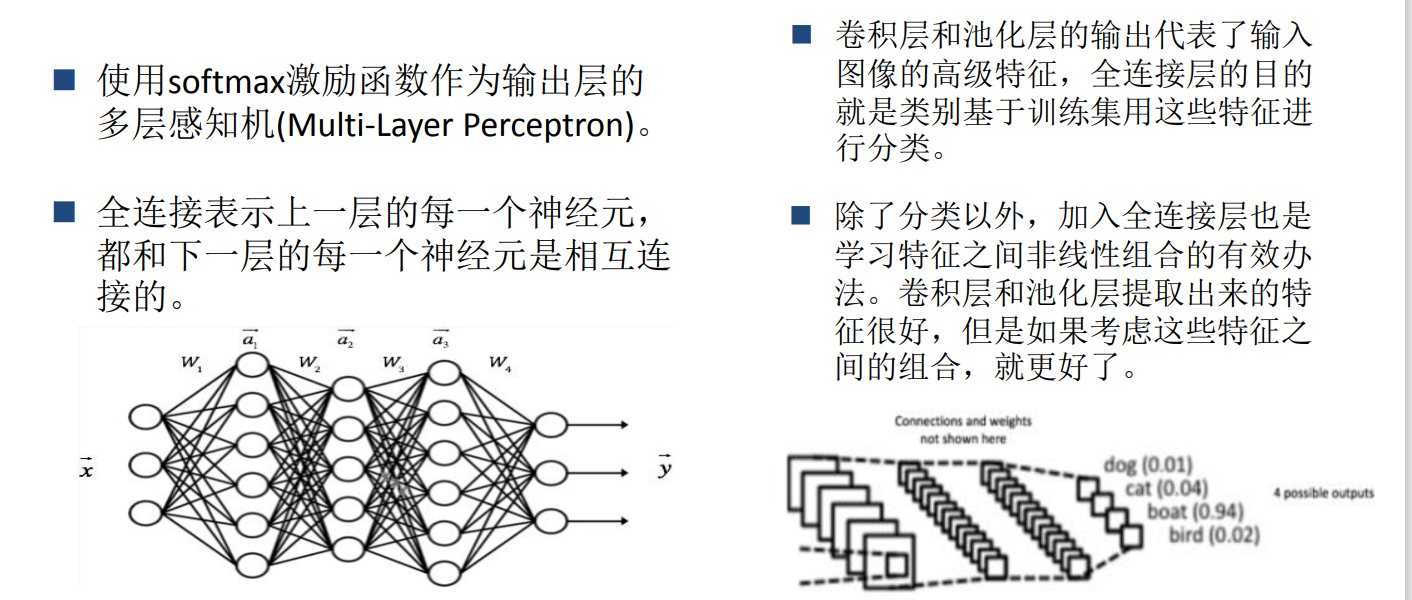
卷积层主要是进行特征获取的,在经过两对卷积池化操作之后完成了特征获取工作,为了实现最终的分类任务,就要通过全连接层神经网络进行拟合来完成分类工作。
这里有一个问题,全连接层的输入是一个向量,而我们经过卷积池化操作以后得到的是16个通道的的矩阵编码,所以我们将这16个矩阵进行拉直操作,使其变平为长度为400的向量。
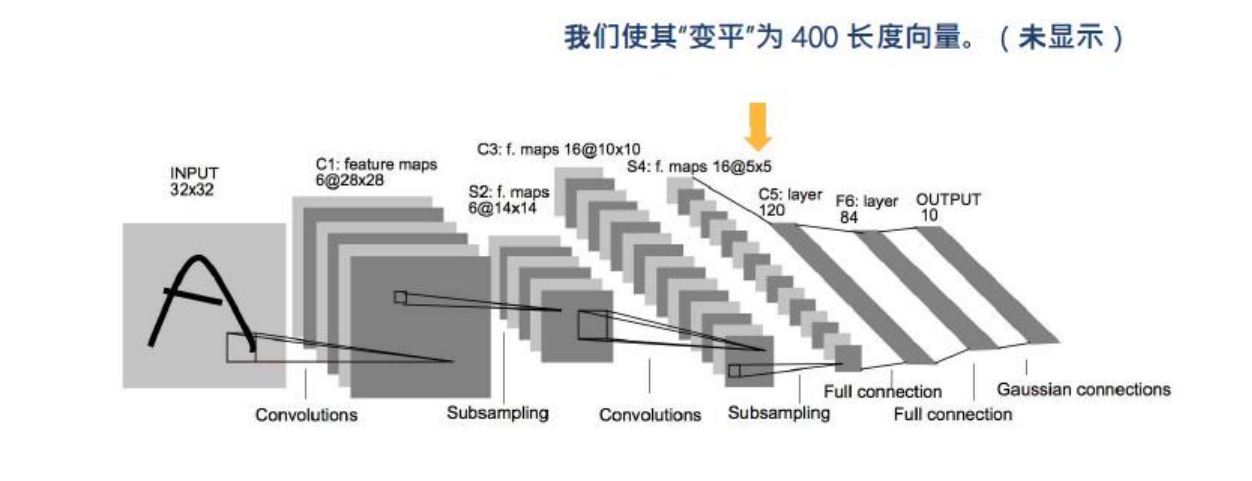
为了更还得进行拟合映射,我们使用了两层全连接层,最后一层采用了softmax函数进行分类输出。
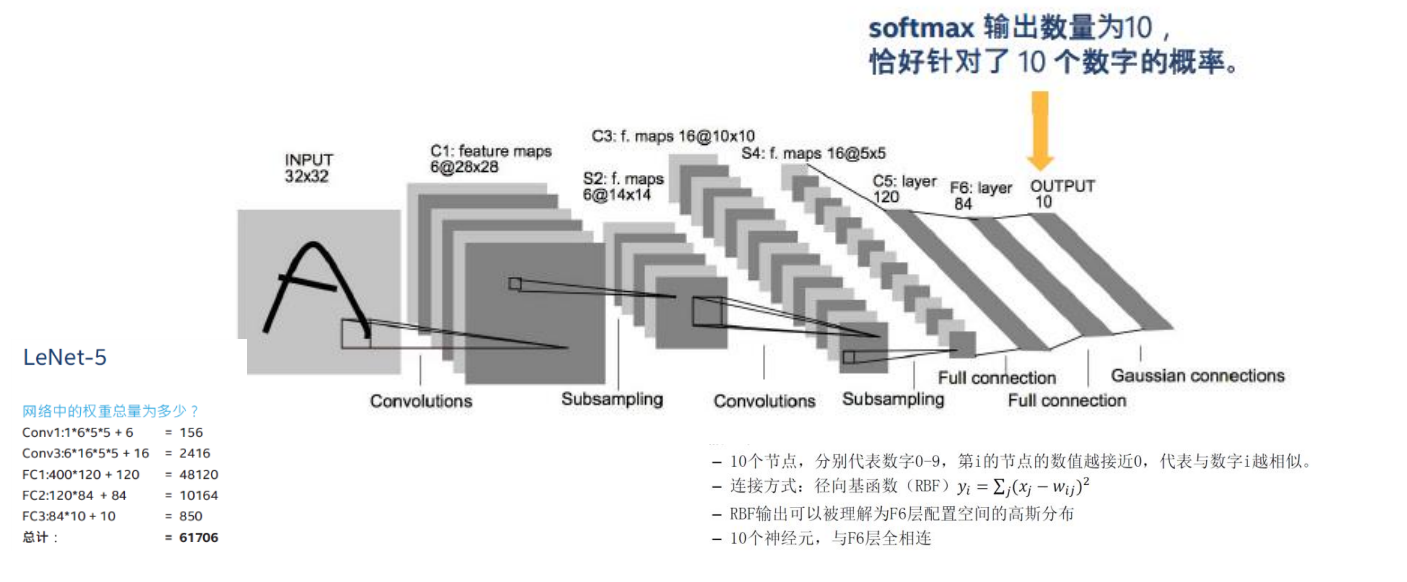
对于卷积神经网络的优化仍然采用前向传递与反向传播的方法进行优化。
完整的卷积神经网络
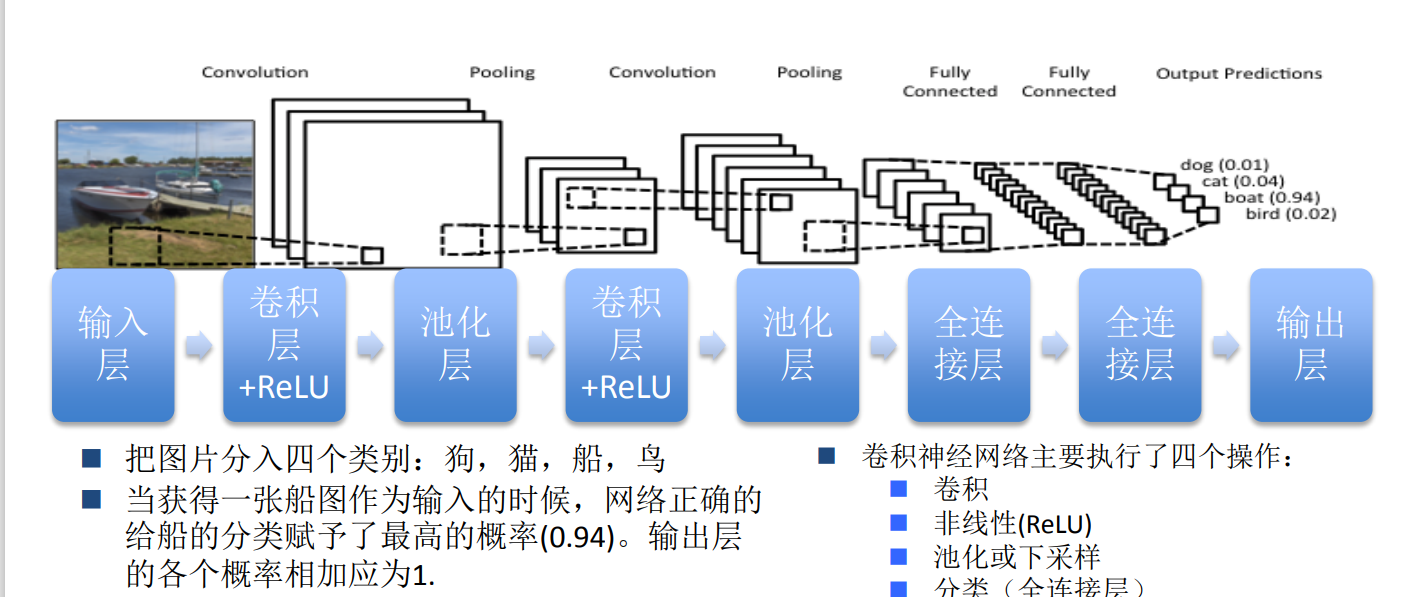
一个完整的卷积神经结构如上图所示:通过卷积层和池化层进行特征提取,之后经过全连接层进行分类。

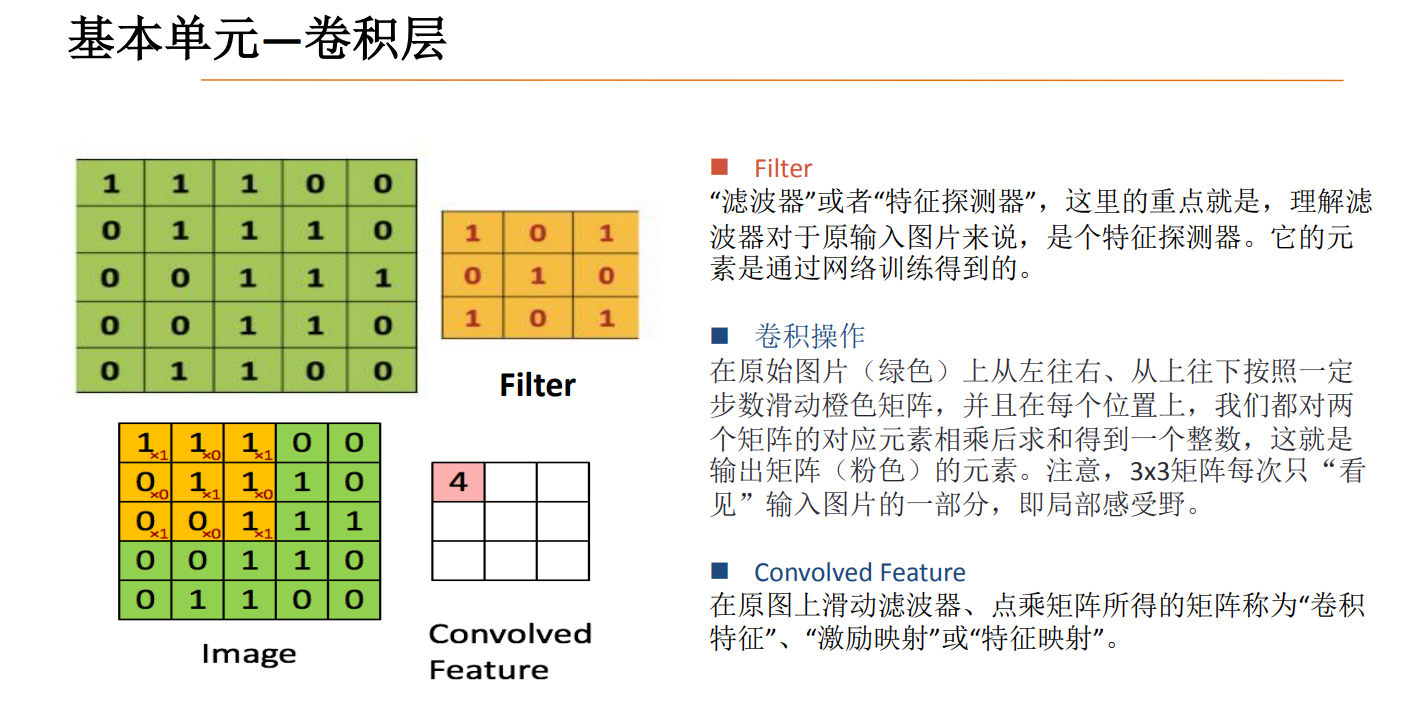
卷积核大小不一样,效果也会不一样。卷积核越小,获得的特征就会越细腻,正确率也会提高,但计算速度就会越来越慢。
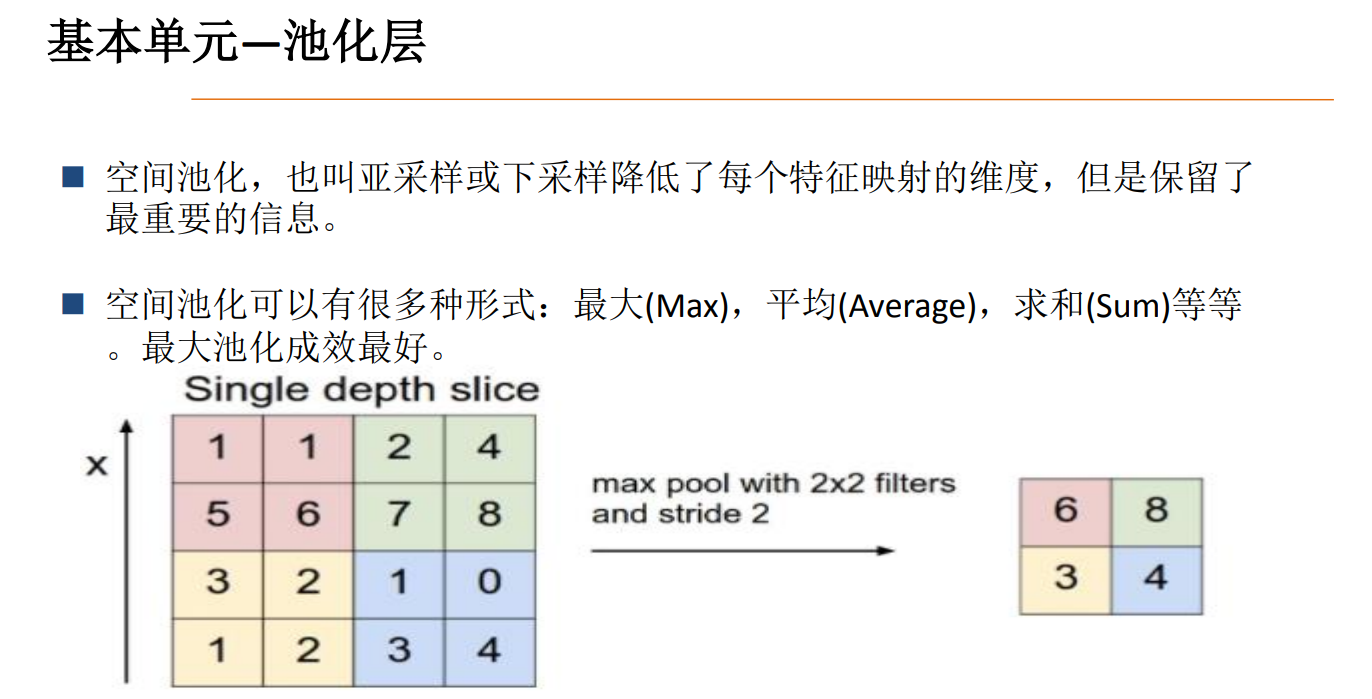
池化操作的特征损失最多,所以在卷积神经网络中不要用过多层的 池化。
对于卷积神经网络来说,仍然采用反向传播的方法进行训练,对参数进行优化。

keras实现卷积神经网络
1 | from tensorflow.python.keras.utils.np_utils import to_categorical |
1 | (train_imgs,train_labels),(test_images,test_labels)=mnist.load_data() |
(60000, 28, 28) (10000, 28, 28)

array([5, 0], dtype=uint8)
1 | train_imgs=train_imgs.reshape((-1,28,28,1)).astype('float')/255#归一化 |
(60000, 28, 28, 1)
(10000, 28, 28, 1)
1 | print(train_labels[:2]) |
[5 0]
(60000, 10)
array([[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)
1 | network=models.Sequential() |
1 | #编译 |
1 | network.fit(train_imgs,train_labels,epochs=10,batch_size=128,verbose=2) |
Epoch 1/10
469/469 - 93s - loss: 2.3410e-04 - accuracy: 0.9999 - 93s/epoch - 198ms/step
Epoch 2/10
469/469 - 93s - loss: 2.1322e-04 - accuracy: 0.9999 - 93s/epoch - 198ms/step
Epoch 3/10
469/469 - 91s - loss: 2.1663e-04 - accuracy: 0.9999 - 91s/epoch - 195ms/step
Epoch 4/10
469/469 - 92s - loss: 1.9149e-04 - accuracy: 0.9999 - 92s/epoch - 196ms/step
Epoch 5/10
469/469 - 96s - loss: 1.7876e-04 - accuracy: 0.9999 - 96s/epoch - 206ms/step
Epoch 6/10
469/469 - 92s - loss: 2.1354e-04 - accuracy: 0.9999 - 92s/epoch - 195ms/step
Epoch 7/10
469/469 - 92s - loss: 1.8261e-04 - accuracy: 0.9999 - 92s/epoch - 195ms/step
Epoch 8/10
469/469 - 91s - loss: 1.8269e-04 - accuracy: 0.9999 - 91s/epoch - 194ms/step
Epoch 9/10
469/469 - 93s - loss: 1.7640e-04 - accuracy: 0.9999 - 93s/epoch - 198ms/step
Epoch 10/10
469/469 - 93s - loss: 1.6239e-04 - accuracy: 0.9999 - 93s/epoch - 198ms/step
<keras.callbacks.History at 0x7f44cd36b910>
1 | print(network.summary()) |
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_2 (Conv2D) (None, 26, 26, 30) 300
max_pooling2d_2 (MaxPooling (None, 13, 13, 30) 0
2D)
conv2d_3 (Conv2D) (None, 13, 13, 60) 16260
max_pooling2d_3 (MaxPooling (None, 7, 7, 60) 0
2D)
flatten (Flatten) (None, 2940) 0
dense (Dense) (None, 500) 1470500
dense_1 (Dense) (None, 10) 5010
=================================================================
Total params: 1,492,070
Trainable params: 1,492,070
Non-trainable params: 0
_________________________________________________________________
None
1 |
|
[[0.00000000e+00 0.00000000e+00 0.00000000e+00 5.90898595e-37
0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00
0.00000000e+00 3.07712727e-38]
[0.00000000e+00 0.00000000e+00 1.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[7.03540223e-29 1.00000000e+00 2.19157929e-22 1.99423557e-32
7.30400380e-22 2.48720310e-24 2.71051034e-19 4.11125203e-21
1.00364764e-19 5.16990182e-28]
[1.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 1.45525489e-34 7.21344118e-27 0.00000000e+00
0.00000000e+00 1.06836722e-30]
[0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
1.00000000e+00 7.54511409e-31 1.74958135e-36 0.00000000e+00
0.00000000e+00 2.67243355e-24]] [[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
[0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]]
313/313 [==============================] - 7s 22ms/step - loss: 0.1187 - accuracy: 0.9904
test_loss: 0.11865610629320145 test_accuracy: 0.9904000163078308

